3 lip 21:42
Mila:
Podpowiedź:
Narysuj prostą równoległą do podstawy i przechodzącą przez wierzchołek szukanego kąta.
3 lip 23:35
suchy: I jak poprowadzę to co dalej?
4 lip 11:02
Bogdan:
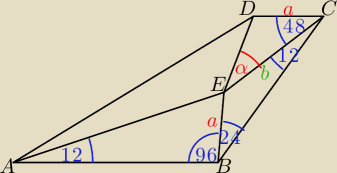
Z oznaczeń na rysunku ( dwie pionowe kreseczki ||) na odcinkach BE i CD domyślam się, że
te odcinki są równej długości: |BE| = |CD| =
a.
Ponadto oznaczam długość odcinka CE literką
b, |CE| = b oraz |∡CDE| = 132 − α
sin(132 − α) = sin132*cosα − sinα*cos132 = sin48*cosα + sinα*cos48
Z twierdzenia sinusów w trójkącie:
| | b | | a | | a*2*sin12*cos12 | |
BCE: |
| = |
| ⇒ b = |
| = 2a*cos12; |
| | sin24 | | sin12 | | sin12 | |
| | a | | b | |
CDE: |
| = |
| ⇒ 2a*cos12*sinα = a*sin(132−α) |
| | sinα | | sin(132−α) | |
2sinα*cos12 = sin48*cosα + sinα*cos48 /:cosα ⇒ 2tgα*cos12 = sin48 + tgα*cos48
4 lip 13:23
Bogdan:
| | sin48 | |
tgα = |
| = tg30 |
| | 2cos12 − cos48 | |
4 lip 13:24
Bogdan:
rysunek się nie wczytał
4 lip 13:25
Bogdan:
4 lip 13:28
Mila:
Zgadza się

4 lip 20:47
Mila:
Pozwolę sobie dokończyć rachunki:
tgα=
| | sin48 | |
= |
| = |
| | cos12+(cos12−cos48) | |
| | sin48 | |
= |
| = |
| | cos12−2sin30*sin(−18) | |
⇔
α=30
0
=====
4 lip 22:57

