Prawdopodobieństwo PR kostka 4 punkty
Damian#UDM: (0−4)
Ze zbioru liczb { 1, 2, 3, 4, 5, 6, 7, 8 } wybieramy losowo jednocześnie cztery liczby. Oblicz
prawdopodobieństwo zdarzenia A polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3
lub największą wylosowaną liczbą będzie 7.
2 lip 01:25
aniabb: 45/70
2 lip 02:30
Damian#UDM: Dziękuje za odpowiedź

Jak to rozwiązać? To najbardziej mnie nurtuje

2 lip 11:22
aniabb:
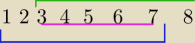
zielone + niebieskie − fioletowe
2 lip 11:29
123: A− najmniejsza to 3
B− najwieksza to 7
teraz wzór
|Ω|=8*7*6*5
P(A∪B)=P(A)+P(B)−P(A∩B)
|A|=6*5*4*3
|B|=7*6*5*4
A∩B=5*4*3*2
Podstaw do wzoru....
2 lip 11:34
Damian#UDM: | | 360 + 840 − 120 | | 1080 | |
P(A∪B) = P(A) + P(B) − P(A∩B) = |
| = |
| = U{ 45 }{ 70 |
| | 1680 | | 1680 | |
}
2 lip 14:50
Damian#UDM: | | 360 + 840 − 120 | |
P(A∪B) = P(A) + P(B) − P(A∩B) = |
| = |
| | 1680 | |
Aniu, niestety Twojego sposobu nie rozumiem do końca, lecz rozwiązanie na zbiorach 123 jest
świetne

Dziękuję wam obu, w końcu to rozumiem!
2 lip 14:52
Damian#UDM: Rozpisałem sobie to wszystko ładnie w diagramie Venna i zauważyłem zachodzące zależności.
2 lip 14:53
Damian#UDM: W sumie Ani sposób też już rozumiem, przedstawione tylko inaczej

2 lip 14:53
 Jak to rozwiązać? To najbardziej mnie nurtuje
Jak to rozwiązać? To najbardziej mnie nurtuje 
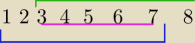 zielone + niebieskie − fioletowe
zielone + niebieskie − fioletowe
 Dziękuję wam obu, w końcu to rozumiem!
Dziękuję wam obu, w końcu to rozumiem!
