elipsa i styczne do niej Liczba_π: Znaleźć iloczyn odległości od ogniska danej elipsy do dwóch dowolnych równoległych stycznych do tej elipsy. Proszę o jakieś podpowiedzi.

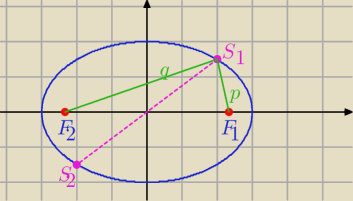
Mila: 1) F₁=(c,0) , F₂=(−c,0) c²=a²−b² c=√a²−b² 2) S=(x_s,y_s)∊ elipsy − punkt styczności S'=(−x_s,−y_s}

x2		y2
	+		=1 równanie elipsy
a2		b2

p+q=2a − suma odległości dowolnego punktu elipsy od F₁ i F₂ jest stała i równa długości osi wielkiej ( 2 a ) . 3) Równanie stycznej przechodzącej przez S:

	x*xs		y*ys
s1:		+		=1⇔
	a2		b2

xs		ys
	x +		*y−1=0
a2		b2

Równanie stycznej przechodzącej przez S':

	−x*xs		−y*ys
s2:		+		=1⇔
	a2		b2

−xs		−ys
	x +		*y−1=0
a2		b2

4) Teraz odległość F₁ od prostej s₁ i odległość F₂ od prostej s₂ Dalej sam może policzysz ?

	x2		y2
Na rysunku jest elipsa o równaniu:		+		=1
	9		4