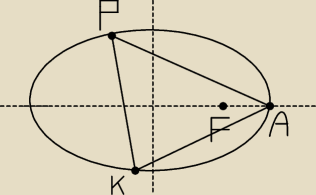
Trójkąt równoboczny wpisany w elipsę M.B:

	x2		y2
W elipsę		+		=1 wpisano trójkąt równoboczny, jeden z jego wierzchołków pokrywa
	36		9

się z prawym wierzchołkiem osi wielkiej. Znaleźć pozostałe wierzchołki trójkąta. Wiem, że A(6,0), F(3√3,0), P(x,y) K(s, t) Próbowałem wyliczyć z tego, że suma długości od P do ognisk jest równa 12 oraz z własności |PA|=|PK|=|AK| niestety wychodzą mi dość skomplikowane rzeczy i nie mogę dojść do niczego sensownego. Czy ktoś mógłby pomóc z góry dzięki odpowiedzi

Qulka: s=x t=−y

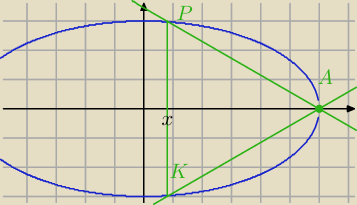
Qulka: albo że prosta KA nachylona jest pod kątem 30°

Qulka: więc KA ma równanie y=√3(x−6)/3 PA ma równanie y=−√3(x−6)/3 podstawiając do równania elipsy : K(6/7 ; −12√3/7) oraz P(6/7 ; 12√3/7)

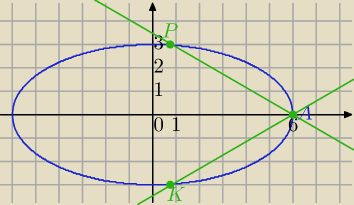
Mila: Podpowiedź; 1) równanie prostej AK:

	√3
y=		x−2√3
	3

2) równanie prostej AP

	√3
y=−		x+2√3
	3

Mila: Należy potem sprawdzić, czy otrzymasz Δ równoboczny.