kwadaty spray: Wykaż że suma pol szarych trójkątów jest równa polu czarnego trójkąta. https://images91.fotosik.pl/387/3c016c0232e9195agen.png Te kwadraty sa takie same i tak ułożone jak na rysunku.

Maciess: Widzisz ze te trzy trojkaty są podobne (KKK)?

spray: widze ze te wieksze sa podobne

spray: i jak wzkaac?

a7: ponieważ trudno mi tu narysować więć, opiszę niech pole czarnego trójkąta to P , pole większego szarego trójkąta P₁, mniejszego szarego trójkąta P₂, pole "gornego" P₃ pole prawego wewnętrznego trójkąta P₄ bok kwadratu to a pole dwóch kwadratów to 2a² , jest równe polu kwadratu którego podstawa jest "na dole" a² oraz pole drugiego kwadratu (przechylonego) czyli P₁+P₂+P₃+a²−P−P₄ czyli 2a²=a²+a²−P−P₄+P₁+P₂+P₃ czyli P₁+P₂=P+P₄−P₃ teraz wystarczyłoby wykazać, że P₄=P₃ jednak P₃>P₄, gdyż P₃ jest podobny do P₄ (k,k,k), ale nie w skali 1, gdyż P₃=1/2*a*h₃, a P₄≠1/2a*h₃ (podstawa przeciwprostokątna P₄ jest mniejsza niż a) dlatego P₁+P₂≠P

spray: Czyli błąd w zadaniu

a7: Może jeszcze ktoś potwierdzi, ale na to wygląda...

Qulka: na pewno są takie same? bo na rysunku ten skośny trochę większy, a dwóch takich samych nie bardzo udaje się tak ułożyć jak te

spray: Qulka o które chodzi?

a7: chodzi o to czy te kwadraty są na pewno takie same

spray: A dla innych kwadratów niekoniecznie takich samych?

spray: Te kwadraty sa podobne.

spray: Mam wskazówke ze ten bordowy dorysowany trójkąt jest taki sam jak ten mniejszt szary. Oraz ten dwa trójkąty bordowy+szary=ciemniejszemu szaremu trójktowi.

spray: https://images92.fotosik.pl/389/5c7380dad586b1e1.png

spray : Ktoś pomoże

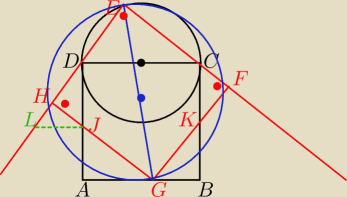
an: Widzę taką konstrukcję: mamy kwadrat ABCD rysujemy okrąg o średnicy DC na łuku DC obieramy dowolny punkt E z którego prowadzimy półproste EH oraz EC otrzymujemy kąt prosty DEC prowadzimy dwusieczną kąta DEC, która przecina bok AB w punkcie G kreślimy okrąg o średnicy EG otrzymujemy punkty FH a następnie kwadrat EHGF.Teraz pogłówkuj jak udowodnić, że △CFK=△LJH i △LJD=△JAG