Całka, pole obszaru ograniczonego
maelle: Obliczyć pole obszaru ograniczonego wykresami funkcji:
y=x2−3x−4 oraz oś Ox
26 cze 17:26
daras: w czym problem
26 cze 17:39
maelle: Chciałem żeby ktoś mi to rozwiązał abym mógł porównać czy dobrze wszystko robię.
26 cze 17:48
WhiskeyTaster: Napisz, co robisz i zweryfikujemy
Tak jest łatwiej zobaczyć Twój punkt widzenia.
26 cze 17:54
Jerzy:
Jakie masz granice całkowania ?
26 cze 17:57
Iryt:
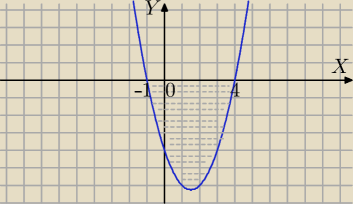
x
2−3x−4=0
x=−1 lub x=4
| | 1 | | 3 | |
−1∫4(0−(x2−3x−4) dx=−1∫4(−x2+3x+4)dx=[− |
| x3+ |
| x2+4x]−14= |
| | 3 | | 2 | |
| | 1 | | 3 | | 1 | | 3 | |
=− |
| *64+ |
| *16+16−(− |
| *(−1)+ |
| *1−4]= |
| | 3 | | 2 | | 3 | | 2 | |
| | 64 | | 1 | | 3 | |
=− |
| +24+16− |
| − |
| +4= |
| | 3 | | 3 | | 2 | |
26 cze 19:44