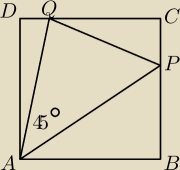
Punkty P i Q leżą odpowiednio na bokach BC i CD kwadratu ABCD przy czym ∡PAQ = 45
(jak na rysunku). Dowieść, żę BP+DQ=PQ
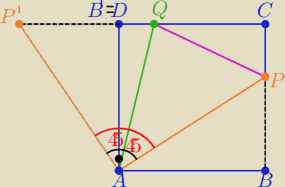Obracając trójkąt ABP o kąt 90o wokół punktu A
otrzymujemy ΔADP' ≡ ΔABP ( bo obrót jest izometrią )
zatem |P'D|=|BP| i |AP'|=|AP|
Trójkąty APQ i AP'Q są przystające z cechy (bkb)
bo |AP'|=|AP| i |AQ| −− wspólny i kąt między tymi bokami 45o
to |P'D|+|DQ|=|PQ| i |P'D|=|BP|
i mamy tezę |BP|+|DQ|=|PQ|
================
