równanie |||: Niech a, b, c>0 rzeczywiste. Istnieje nieskończenie wiele liczb całkowitych x, y które spełniają nierówność a^x>cb^y jeśli: a) a>1 lub b < 1 b) a<1 lub b<1 c) a<1 oraz b<1 d)a<1 oraz b>1 ? Jak to rozwiązać i dojść do właściwej odpowiedzi?

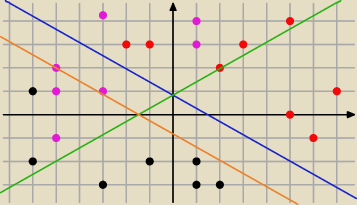
Qulka: a) dla a=3 i b=1/7 (nad niebieską) jest nieskończenie dużo czerwonych kropek b) dla a=1/3 i b=1/7 (nad zieloną) jest nieskończenie dużo fioletowych kropek c) dla a=1/3 i b=1/7 (nad zieloną) jest nieskończenie dużo fioletowych kropek c) dla a=1/3 i b=7 (pod pomarańczową) jest nieskończenie dużo czarnych kropek

|||: Nie rozumiem twojego toku.

wredulus_pospolitus: dla każdego podpunktu można tak dobrać a i b, aby nierówność zachodziła dla nieskończonej liczby x i y

Qulka: nawet szczególnie dobierać nie trzeba było za c chyba wstawiłam 5

|||: Ale tu nie chodzi o podanie przykładu tylko w którym z tych przypadków dla kazdego takiego a oraz b.

Bleee: Treść tego nie mówi. To żeby uszczegółowić − chodzi oto, aby istniało nieskończenie wiele przyporzadkowanych par postaci (x.y) które będą spełniać nierówność z treści dla DOWOLNYCH a, b, c spełniających tylko i wyłącznie powyższe nierówności? Jeżeli tak to..... dla żadnej z tych odpowiedzi nie powinno wyjść.

|||: Blee a czemu dla zadnej nie zachodzi?

Qulka: nie podawałam przykładu tylko pokazywałam że dla każdego są bo niezależnie jak bardzo się wygną to znajdę takie punkty gdyż różnica była tylko w kierunku i wyboru półpłaszczyzny ale nadal istnieje nieskończenie wiele takich par całkowitych (x,y)

wredulus_pospolitus: @Qulka −−− tylko chodzi oto, że autor chce mięć nieskończenie wiele par (x,y) dla których (już ustalonych par) zachodzi powyższa nierówność dla DOWOLNYCH a,b,c (spełniających nierówności podane w danych podpunktach) a to już diametralnie zmienia postać rzeczy.

|||: tak dzieki wredulus_pospolitus Właśnie jak dojść do tej zależności.

Qulka: to zależy które pary wybierze

|||: jakie pary?

wredulus_pospolitus: załóżmy, że jest taka para (x_o , y_o) dla której DLA DOWOLNEGO a,b,c spełniona jest powyższa nierówność. to oznacza, że: 1. w podpunkcie (c) nierówność ma być spełniona także dla takich wartości: a = b = 0 ; c > 0 a^x_o > c*b^y_o 0 > c*0 0 > 0 sprzeczność 2. z tego samego powodu mamy sprzeczność w (b) bo także tak dobrane a, b, c spełniają warunek nałożony w (b) 3. natomiast w (d) musi być spełniona nierówność dla chociażby: a = 0 ; b > 1 ; c > 0 0 > c*b^y_o > 0 <−−− sprzeczność 4. pozostaje nam jedynie (a) gdzie mamy: a > 1 lub b < 1 ale tutaj zauważ, że masz lub więc dana wartość musi być spełniona także dla takiego 'zestawu' a,b,c: a < 1 , b < 1 i c > 0 a to wiemy że jest sprzeczne (parz 1.)

wredulus_pospolitus: w efekcie −−−− nie istnieje ani jedna taka para (x_o , y_o) aby spełniona była powyższa nierówność dla DOWOLNYCH a,b,c spełniających warunki: c > 0 ; a,b w zależności od podpunktu

|||: natomiast w (d) musi być spełniona nierówność dla chociażby: a = 0 ; b > 1 ; c > 0 Czemu mozesz to wyjasnic bardziej.

Bleee: 0 = a < 1 b>1 Czyli spełnione warunki podpunktu są więc nierówność też musi być spełniona, a nie jest.

Qulka: w treści jest że abc są WIĘKSZE od zera

Qulka: a^x>cb^y //log xloga>logc+ylogb ylogb<xloga−logc i tu w kwestii dzielenia jest ta różnica że jak b<1 czyli logb<0 to zmieniasz znak więc albo nad albo pod y< lub > xlog_ba−log_bc no i teraz zaleznie od a i b współczynnik przed x jest różny ale w tych zakresach zawsze się znajdzie jakaś ćwiartka pasująca do tego pęku prostych

lll: Czyli nie da się jednoznacznie określić która z tych odpowiedzi jest poprawna

Bleee: @Qulka, dla mnie zapis a, b, c>0 rzeczywiste oznaczał ze jedynie c ma nałożony warunek bycia liczba dodatnia

lll: Ten zapis znaczy że te trzy są dodtatnie

Qulka: nie umiem zrobić nierówności więc tam trzeba sobie wyobrażać czy nad czy pod ale można trochę posprawdzać https://www.geogebra.org/geometry/pxkawcek

wredulus_pospolitus: Jeżeli przyjmiemy, że a>0 , b>0 , c>0 to warunki początkowe nadal ŻADNA z odpowiedzi nie pasuje. Weźmy jakąś parę (x_o , y_o) dla której spełniona jest nierówność a^x < c*b^y dla jakiś dodatnich a₀, b₀, c₀ które dodatkowo spełniają warunki z danego podpunktu Wykaże, że wtedy istnieje taki zbiór (a₁, b₁, c₁) dla których powyższa nierówność NIE BĘDZIE spełniona dla tejże pary (x₀ , y₀). Niech: a₁ = a₀ (czyli a₁^x_o = a₀^x_o) b₁ = b₀ (czyli b₁^y_o = b₀^y_o)

	a0xo
c1 =
	b0yo

i wtedy mamy: L = a₁^x_o = a₀^x_o P = c₁ * b₁^y_o = c₁ * b₀^y_o = a₀^x_o L = P <−−− sprzeczność oczywiście warunek c₁ > 0 jest spełniony (ponieważ a₁ = a₀ i b₁ = b₀ są liczbami dodatnimi).

|||: ok dzieki