zbiory anonim123: Jak narysować zależność w zbiorach A iloczyn (BsumaC)=(AiloczynB)suma(AiloczynC)

Qulka: https://prnt.sc/t1n4em

anonim123: A jak mam rozumieć że na zbiorach dodawanie jest rozdzielne względem mnożenia A∪(B∩C)=(A∪B)∩(A∪C) bo jak zamienię to tak A+(BC)=(A+B)(A+C) to nic nie wychodzi?

Jerzy: Bo jakim cudem ma wyjść ? Czy: 2 + 3*4 = (2 + 3)*(2 + 4) ?

anonim123: No tak się nie da. To w takim razie jak to poprawnie wykonać?

ite: Obejrzyj najpierw ten film od działaniach na zbiorach: https://www.youtube.com/watch?v=MgPKtWV2wiE Potem pod koniec tego znajdzisz wytłumaczenie rozdzielności sumy zbiorów względem ich iloczynu https://www.youtube.com/watch?v=kGafQcnOcM8&list=PLjUjmsuTACB7vaHaf_-kdDOhQ4E4_7aCP&index=15 To są inne działania i mają inne właściwości niż dodawanie i mnożenie liczb rzeczywistych!

anonim123: Dziękuję

anonim123: jak udowodnić A∩(B∪C)=(A∩B)∪(A∩C) (A∩B)∪(A∩C) ja zaczęłam tak x należy do A i x należy do B lub x należy do A i x należy do C?

Qulka: https://prnt.sc/t20wwe

anonim123: Dziękuję. A jak za pomocą rachunku zdań udowodnić <2,5>∪<3,7>=<2,7>?

anonim123: ?

Qulka: tak samo

anonim123: A ktoś mógłby to policzyć, bo nie bardzo wiem jak to zrobić?

Qulka: x∊<2,5>vx∊<3,7>⇔(x≥2 ∧ x≤5) v (x≥3 ∧ x≤7) ⇔ (x≥2 v x≥3) ∧ (x≤5 v x≤7) ⇔ x≥2 v x≤7⇔x∊<2,7>

anonim123: Skąd jest (x≥2 v x≥3) ∧ (x≤5 v x≤7) ?

anonim123: ?

Qulka: z podwójnej rozdzielności (x≥2 ∧ x≤5) v (x≥3 ∧ x≤7) ⇔ (x≥2 ∧ x≤5) v (x≥3) ∧ (x≥2 ∧ x≤5) v ( x≤7) ⇔ (x≥2 v (x≥3) ∧ (x≤5) v (x≥3) ∧ (x≥2 ) v ( x≤7) ∧ ( x≤5) v ( x≤7) ⇔ (x≥2) ∧ R ∧ R ∧ ( x≤7) ⇔ x≥2 ∧ x≤7⇔ x∊<2,7> mówiłam że to po prostu pisanie tego samego do bólu aż się znaczki plączą

anonim123: A co oznacza R?

Qulka: zbiór liczb rzeczywistych

anonim123: A dlaczego tam występuje?

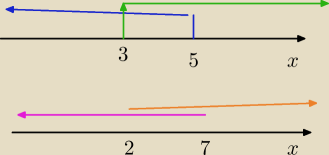
Qulka: bo (x≤5) v (x≥3) jak widać na górnym to wszystkie x bo (x≥2 ) v ( x≤7) jak widać na dolnym to wszystkie x

anonim123: A dlaczego znika (x≥3) i ( x≤5) w ostatniej linijce obliczeń?

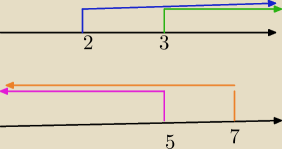
Qulka: bo (x≥2 v (x≥3) więc sumą jest niebieskie x≥2 górny obrazek bo ( x≤5) v ( x≤7) więc sumą jest pomarańczowe x≤7 dolny obrazek

anonim123: A są na to jakieś reguły lub wzory czy muszę tak to przedstawiać?

Qulka: nie musisz... wystarczy wiedzieć że dlatego znikało

anonim123: A są w ogóle jakieś wzory na to?

Qulka: na co? na te obrazki..dokładnie takie same jak na zbiory suma to wszystko co jakkolwiek zamalowane , część wspólna to to co jednocześnie ma dwa kolory

anonim123: A nie można użyć wzoru (p i (q lub r ) wtedy i tylko wtedy(p i q)suma(p i r)?

Qulka: w którym momencie

anonim123: (x≥2 ∧ x≤5) v (x≥3 ∧ x≤7) po tym?

Qulka: po tym (x≥2 ∧ x≤5) v (x≥3 ∧ x≤7) pisząc podwójna rozdzielność użyłam dwa razy takiego (p lub (q i r ) wtedy i tylko wtedy(p lub q) i (p lub r)

anonim123: nie rozumiem

anonim123: nie widzę tutaj zastosowania tego wzoru, a z twojej wiadomości wynika, że taka istnieje

Qulka: jeszcze raz <2,5>∪<3,7>=<2,7> x∊<2,5> v x∊<3,7> ⇔ (x≥2 ∧ x≤5) v (x≥3 ∧ x≤7) ⇔ teraz (p lub (q i r ) wtedy i tylko wtedy(p lub q) i (plub r) ⇔ (x≥2 ∧ x≤5) v (x≥3) ∧ (x≥2 ∧ x≤5) v (x≤7) ⇔ i znów (x≥2) v(x≥3) ∧ (x≤5) v (x≥3) ∧ (x≥2) v(x≤7) ∧ (x≤5)v(x≤7) (x≥2) ∧ R ∧ R ∧ ( x≤7) ⇔ x≥2 ∧ x≤7⇔ x∊<2,7>

Qulka: doróbki w kolorkach (p lub (q i r)⇔(p lub q) i (p lubr) ⇔ (x≥2 ∧ x≤5) v (x≥3) ∧ (x≥2 ∧ x≤5) v (x≤7) ⇔ i znów (x≥2) v(x≥3) ∧ (x≤5) v (x≥3) ∧ (x≥2) v(x≤7) ∧ (x≤5)v(x≤7) (x≥2) ∧ R ∧ R ∧ ( x≤7) ⇔ x≥2 ∧ x≤7⇔ x∊<2,7>

anonim123: Dziękuję za odpowiedź, ale nadal jeszcze tego nie rozumiem. Dlaczego tutaj jest znak lub a nie znak i tak jak w początkowym we wzorze,który opisujesz? Co tutaj zostało zastosowane (x≥2) v(x≥3) ∧ (x≤5) v (x≥3)?

anonim123: Nie rozumiem dlaczego wzór podany przeze mnie nie ma tutaj zastosowania a twój ma i Co tutaj zostało zastosowane (x≥2) v(x≥3) ∧ (x≤5) v (x≥3)?

Qulka: p to (x≥2) q to (x≥3) r to (x≤5) s to (x≥3) i mamy od początku (p i r ) lub (q i s) rozdzielam czerwone i (p i r ) lub q i (p i r ) lub s i dlatego to nie twój wzór bo twój rozdzielał lub teraz rozdzielam zielone i dwa razy bo są dwa p lub q i r lub q i p lub s i r lub s i te cztery już graficznie albo w pamięci

anonim123: Co znaczy rozdzielam czerwone i?

Qulka: stosuję wzór na rozdzielność alternatywy względem koniunkcji czyli to co pisałam wcześniej (p lub (q i r ) wtedy i tylko wtedy (p lub q) i (plub r) literki takie jak napisałaś na początku to nie te co ostatnio zamiast nawiasów a Twój wzór to była rozdzielność koniunkcji względem alternatywy (p i (q lub r ) wtedy i tylko wtedy (p i q) suma (p i r)

Qulka: dla zbiorów rozdzielność sumy względem iloczynu Au(BnC)=AuB n AuC rozdzielność iloczynu względem sumy An(BuC)=AnB u AnC

anonim123: nie rozumiem tego w ogóle

Qulka: a rozdzielność mnożenia względem dodawania a•(b+c)=a•b +a•c ?

anonim123: to znam

Qulka: to to jest to samo tylko nazwy inne

anonim123: A (p lub (q i r ) to jest (x≥2 ∧ x≤5) v (x≥3 ∧ x≤7)?

Qulka: tak pierwszy nawias to p a drugi to (q i r)

anonim123: A dlaczego pomija się i w nawiasie?

Qulka: nie pomija .. rozbija się potem dlatego pisałam najpierw czerwone i a potem zielone i

Qulka: https://prnt.sc/t3glp7

anonim123: Już trochę więcej rozumiem ale nie wiem dlaczego to nie mój wzór jak tam są spójniki i spojnik lub spójnik i?

Qulka: bo Twój miał lub w nawiasie a mój lub przed nawiasem a tak w ogóle i ten i ten to rozdzielność

anonim123: A dlaczego to nie jest ta część wzoru (p ∧ q) ∨ (p ∧ r) to nie jest(x≥2 ∧ x≤5) v (x≥3 ∧ x≤7)

Qulka: boby jedno p oznaczało dwa różne nawiasy

Qulka: dlatego na tym obrazku p to był ten fioletowy długi prostokąt

anonim123: Ok. A dlaczego nie rozdzielam tego fioletowego prostokąta w początkowej fazie tylko potem?

Qulka: bo tak jest czytelniej i pewniej że się nie pomylimy kolejność była dowolna...można było najpierw fioletowy a potem niebieskie, ale chciałam żeby bardziej pasowało do wzoru bo i tak się zrobił bałagan

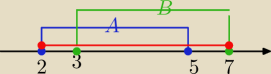
Qulka: poza tym normalnie to się robi rachunkiem zbiorów a nie zdań czyli obrazek czerwony to AuB czyli <2;7>

anonim123: A dlaczego tak podstawiam do wzoru że p = (x≥2 ∧x≤5)?

anonim123: Resztę już rozumiem tylko nie wiem dlaczego to jest tak podstawione do wzoru?

Qulka: bo to po prostu pierwszy nawias a postanowiłam najpierw rozpisać drugi żeby wyglądało tak jak we wzorze że to drugi się rozdziela ale jak mówiłam kolejność jest dowolna można zrobić wszystko odwrotnie ale już nie mieszajmy

anonim123: ale jak tam po środku jest spójnik i w nawiasie to dlaczego można to podstawić do wzoru?

Qulka: które i bo są dwa... podstawiłam do wzoru oba tylko najpierw pierwszy a potem drugi żeby się nie pogubić bo jak zrobiłam od razu to nie dość że wstawiłam inny znaczek to jeszcze i tak potem musiałam wyjaśniać z skąd to tak więc tym razem zrobiłam powoli każde osobno

Qulka: a jeśli się pytasz dlaczego cały nawias ze spójnikiem w środku jako jedno P to dlatego że jest to nawias i możemy go potraktować jak całość (bo po to są nawiasy )

anonim123: Dziękuję