Pomoże ktoś? slipknot96: Zbadaj monotoniczność funkcji. a) f(x)= ^√x_lnx b) f(x)= xlnx c) f(x)= xe^x2

slipknot96: c) f(x)= xe^x2−3x

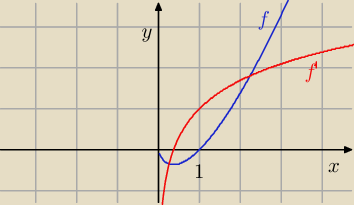
janek191: b) f(x) = x ln x x > 0 f '(x) = ln x + 1 > 0 ⇔ ln x .> − 1 ⇔ ln x > ln e⁻¹ ⇔ x > e⁻¹ zatem f rośnie w ( e⁻¹ , +∞) a maleje w ( 0, e⁻¹)

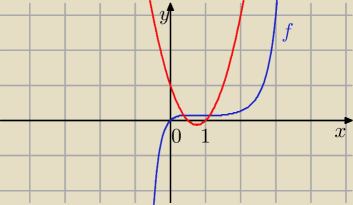
janek191: f(x) = x*e^{x2 − 3 x} f '(x) = ( 2 x² −3 x + 1)*e^{x2 −3 x} e^{x2 −3 x} > 0 więc

	1
f '(x) > 0 ⇔ x2 − 3 x + 1 > 0 ⇔ x ∊( − ∞,		) ∪ (1. +∞)
	2

wtedy f rośnie.

	1
f '(x) < 0 ⇔ x ∊ (		, 1 )
	2

wtedy f maleje.

janek191: ?

styropian999: a ,,a" umiesz?

janek191: Za b i c nie miał kto podziękować

Jerzy: Potrafisz ustalić dziedzinę i policzyć pochodną ?

ICSP: on nie chce zrozumieć i spróbować tylko chce gotowe rozwiązania.

	√x
a) f(x) =
	ln(x)

D : x > 0 i x ≠ 1

	ln(x) − 2
f'(x) =
	2√xln2(x)

funkcja maleje gdy ln(x) − 2 < 0 x < e² i x > 0 i x ≠ 1 Czyli jest malejąca przedziałami: x ∊ (0 ; 1) , x ∊ (1 ; e²) funkcja rośnie gdy ln(x) − 2 > 0 x > e²