Olbicz pole kwadratu
esper:
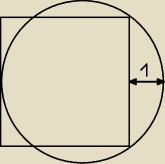
Oblicz pole kwadratu
16 cze 15:39
Bleee:
Zaznacz środek okręgu, poprowadź odcinek do prawego górnego wierzchołka a drugi do strzalki
Masz trójkąt prostokątny o bokach:
r − − − przeciwprostokatna
r−1 − − − przyprostokatna (która rysowałeś)
(2r−1)/2 − − − druga przyprostokatna (połowa boku trojkata)
Wyznacz 'r' z tw. Pitagorasa.
16 cze 16:21
a7:
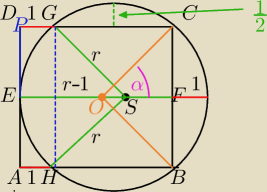
P=(2r−1)
2
| | CF | | r−1/2 | |
sinα=sin45=√2{2}= |
| = |
| ⇒ r=1+√2{2} |
| | OC | | r | |
P=(2+
√2−1)
2=3+2
√2
16 cze 16:35
esper: dzięki ziomeczki
16 cze 17:41
a7: chwilka, u mnie błąd OC≠r
16 cze 17:42
Iryt:
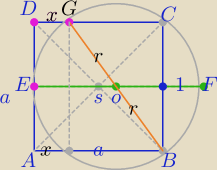
|EO|=|OF|=r
|∡ACB|=90
o
1) z tw. o stycznej i siecznej
| | 3 | |
2) W ΔBCG: (2r)2=a2+( |
| a)2 |
| | 4 | |
| | 25 | | 5 | | 5 | |
4r2= |
| (2r−1)2⇔r= |
| ∉D lub r= |
| |
| | 16 | | 18 | | 2 | |
a=4
P
□=16
=====
16 cze 20:59
Eta:
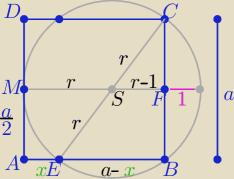 2 sposób
2 sposób
a=2r−1 , r>1/2 , |AE|=x , |EB|=a−x
Z podobieństwa trójkątów EBC i SFC w skali k=2
a−x= 2(r−1) ⇒ 2r−1−x=2r−2 ⇒
x=1
i z tw. o stycznej i siecznej
|AM|
2=|AE|*|AB|
| | a | |
( |
| )2=1*a ⇒ a2=4a ⇒ a=4 |
| | 2 | |
P□= 16
=======
16 cze 22:28
Mila:
Zmieniłam oznaczenia i w 20:59 ma być usunięty zapis : ∡ACB|=90o .
16 cze 22:36
 Oblicz pole kwadratu
Oblicz pole kwadratu
 P=(2r−1)2
P=(2r−1)2
 |EO|=|OF|=r
|∡ACB|=90o
|EO|=|OF|=r
|∡ACB|=90o
 2 sposób
a=2r−1 , r>1/2 , |AE|=x , |EB|=a−x
Z podobieństwa trójkątów EBC i SFC w skali k=2
a−x= 2(r−1) ⇒ 2r−1−x=2r−2 ⇒x=1
i z tw. o stycznej i siecznej
|AM|2=|AE|*|AB|
2 sposób
a=2r−1 , r>1/2 , |AE|=x , |EB|=a−x
Z podobieństwa trójkątów EBC i SFC w skali k=2
a−x= 2(r−1) ⇒ 2r−1−x=2r−2 ⇒x=1
i z tw. o stycznej i siecznej
|AM|2=|AE|*|AB|