Matura rozszerzona
Matfiz: Tych liczb siedmiocyfrowych ile wam wyszło? Mi 12960 a pole ostrosłupa ponad 300
15 cze 12:17
salamandra: Tyle samo w siedmiocyfrowych, w ostrosłupie jakiś kosmos
15 cze 12:19
Matfiz: A wymiary telefonu 6 na 10 cm?
15 cze 12:23
ICSP: Nie
15 cze 12:24
salamandra: Tak, A równanie okręgu (x−10)2+(y−9)2=153?
15 cze 12:27
Poprostupatryk: Tyle samo! Ogłaszam stan powyjątkowy
można się zrelaksować. Łatwy arkusz,
zdążyłem wszystko napisać, sprawdzić
i jeszcze podrapać się po nosie

15 cze 12:28
ICSP: Tak
15 cze 12:28
Matfiz: Tak samo ale promień mam źle
15 cze 12:45
fil: 624 w ostroslupie, albo cos kolo tego
15 cze 12:46
fil: salamanfra jak dowod poszedl?
15 cze 12:46
Chorus: Dowód poziomem podobny do tego na podstawie

15 cze 12:48
Chorus: Jakie były wymiary telefonu? Mi też wyszło 6 10
15 cze 12:50
Matfiz: Mi w ostrosłupie około 370 wyszło
15 cze 12:50
fil:
Wymiary telefonu to 6.6 i 11 jednak pytali nas o wymairy ekranu, czyli 6 i 10
15 cze 12:50
fil:
A kodowane co wpisaliscie?
15 cze 12:51
Matfiz: 891 chyba xD
15 cze 12:52
Matfiz: A w 4 w zamkniętym 36?
15 cze 12:52
Chorus: Tak
15 cze 12:54
Shizzer: Ja w ostroslupie sie skupilem na tym ze w podstawe moglem wpisac okrag i sie na tym caly czas
opieralem. Nie wyznaczylem krawedzi podstaw trapezu, jakos nie moglem nic wymyslic. Dowodu nie
zdazylem z planimetrii bo sb odcinki zle pozaznaczalem. A promien obrazu okregu zrobilem jako
| | 1 | |
|
| promienia okręgu oryginalnego. Nie pamiętałem jak się te promienie z jednokładności |
| | 3 | |
wylicza

Reszta myślę, że ok
15 cze 12:57
Shizzer: O i srodek okregu mi wyszedl 2, 6... dziwne Oo
15 cze 12:58
Poprostupatryk: W kodowaniu 955 dalem
15 cze 12:59
Matfiz: Shizzer tak samo z promieniem, ogólnie moim zdaniem to był bardzo wymagający arkusz

15 cze 13:03
Matfiz: bardzo nieschematyczne i trudne zadania były moim zdaniem
15 cze 13:03
Shizzer: Ten okrag to na pewno mial byc (10, 9)?
15 cze 13:03
Shizzer: Srodek okregu znaczy sie
15 cze 13:03
Matfiz: mi wyszło 10,9 albo 9,10
15 cze 13:07
fil:
(10, 9)
15 cze 13:07
Shizzer: Nie mam pojecia jakim cudem
15 cze 13:08
Matfiz: jak zle zapisalem promien to a srodek okregu dobrze to moge na 4 pkt liczyc? xD
15 cze 13:12
Shizzer: Nagle sie robi wynik 80% jak jeszcze gdzies czegos nie spieprzylem. Ale do dupy
15 cze 13:12
Matfiz: ja chce 70%

bardzo trudny arkusz był
15 cze 13:12
ICSP: 30% będzie
15 cze 13:14
Chorus: W sumie najbardziej ciekaw jestem zadania z kombinatoryki. Mi wyszła jakaś kompletna bzdura
39900, znajomym od 900 ileś po 11tys ileś. Mógłby ktoś rozpisać ładnie Newtonem?
15 cze 13:31
Frajvald: Ja to z siedmiocyfrowych podzieliłem na 3 przypadki
1. na pierwszym miejscu 1
| | | | | |
1* | * | *8*8 // rozstawiam pozostale 2 jedynki na 6 miejsc,2 dwójki na 4, i pozostałe |
| | | |
2 cyfry na 8*8
2.na pierwszym miejscu 2
| | | | | | | | | |
1* | * | *8*8 // rozstawiam dwójke na | miejsc, jedynki na | i pozostałe |
| | | | | |
cyfry(oprócz 1 i 2) na 8*8
3. na pierwszym miejscu ani 2 ani 1 ani 0
| | | | | | | | | |
7* | * | *8 // na pierwszym cyfre na 7 sposobów, jedynki na | , dwójki na | |
| | | | | |
i ostatnia na 8
Wyszlo mi tyle samo co Matfiz i salamandra 12960, wiec chyba jest ok?
15 cze 13:47
salamandra: identycznie zrobiłem
15 cze 13:47
Matfiz: Ja to samo
15 cze 13:48
BoosterXS: Tak samo, 12960

15 cze 13:49
BoosterXS: Jak rozpracowaliście ten dowód geometryczny? jedyne zadanie, którego nie zrobiłem

15 cze 13:50
Frajvald: | | 4 | |
Długo by pisać ale mi wyszło AM =6−(2+√2)=4−√2 a MC= 2+√2 wiec stosunek |
| mi nie |
| | 5 | |
chciał wyjść

15 cze 13:53
Frajvald: I ogólnie ten trójkąt był prostokątny co nie?
15 cze 13:53
Matfiz: mi tez nie wyszlo

15 cze 13:57
Chorus: Ah głupi ja. Zamiast ósemek dałem dziesiątki, zapomniałem że pozostałe liczby nie mogą być ani
2 ani 3.
Ogólnie bardzo proste było zadanie z parametrem prawda? Wyszły dwa rozwiązania tak?
15 cze 14:12
Matfiz: −9/5 i 1/4
15 cze 14:25
getin:
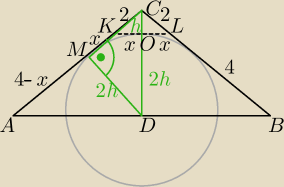
Zad. 7
|AC| = |BC| = 6
|CK| = |CL| = 2
O − środek KL
D − środek AB (środek okręgu)
|MK| = |KO| = |OL| = x
|AM| = |AC| − |MK| − |CK| = 6 − x − 2 = 4−x
|CO| = h
ΔCOL ~ ΔCDB
| |CL| | | |CB| | | 2 | | 6 | |
| = |
| → |
| = |
| → |CD| = 3h |
| |CO| | | |CD| | | h | | |CD| | |
|OD| = |CD| − |CO| = 3h − h = 2h
zatem promień półkola to 2h
układ równań z Pitagorasów w ΔKOC i ΔCMD
{x
2+h
2 = 2
2
{(x+2)
2 + (2h)
2 = (3h)
2
| | 4 | |
wychodzi z niego że x = |
| |
| | 3 | |
| | 4 | | 8 | |
wówczas |AM| = 4 − |
| = |
| |
| | 3 | | 3 | |
15 cze 16:33
Eta:
Zad7 ( korzystam z rys. podanego przez
getin
Można też tak :
1/ Z podobieństwa trójkątów ABC i KLC w skali k=6/2=3 to R=2h , R
2=4h
2 i |DC|=3h
2/ w Δ ADC : R
2= |AM|*|MC| / : |MC|
2
i w Δ DMC : |MC|
2= (3h)
2−(2h)
2 ⇒ |MC|
2=5h
2
i mamy tezę:
============
15 cze 18:07
getin:
ten dzisiejszy geometryczny dowód miał coś wspólnego z tym dowodem z podstawy 9 czerwca
ten na podstawowej nawet w pewnym sensie był trudniejszy
bo tam nie było długości boków wyrażonych konkretną liczbą
niewykluczone że ta sama osoba wymyślała dowody geometryczne dla obu matur
15 cze 18:13
15 cze 18:14
getin:
nie było pochodnej i musieli dać takie żeby z własności funkcji kwadratowej ogarnąć
ale bardzo mnie zdziwiło że na nowej formule było aż 8 zadań na drugą potęgę a ani jednego na
trzecią
miłośnicy delty naprawdę mogli przebierać w zadaniach jak w ulęgałkach
zwolennicy wielomianów 3−go stopnia byli zawiedzeni
15 cze 18:30
123: Dość dużo schematów np 14−ste z ostrosłupem, czesto jest liczona taka objętość.
15 cze 18:38


 Reszta myślę, że ok
Reszta myślę, że ok

 bardzo trudny arkusz był
bardzo trudny arkusz był




 Zad. 7
|AC| = |BC| = 6
|CK| = |CL| = 2
O − środek KL
D − środek AB (środek okręgu)
|MK| = |KO| = |OL| = x
|AM| = |AC| − |MK| − |CK| = 6 − x − 2 = 4−x
|CO| = h
ΔCOL ~ ΔCDB
Zad. 7
|AC| = |BC| = 6
|CK| = |CL| = 2
O − środek KL
D − środek AB (środek okręgu)
|MK| = |KO| = |OL| = x
|AM| = |AC| − |MK| − |CK| = 6 − x − 2 = 4−x
|CO| = h
ΔCOL ~ ΔCDB
 coś chcieli zaniżyć
coś chcieli zaniżyć  https://www.oke.waw.pl/files/oke_waw_2550MMA-R1_1P-202s.pdf.pdf
https://www.oke.waw.pl/files/oke_waw_2550MMA-R1_1P-202s.pdf.pdf