Równania astra: Rozwiąż równanie ||x|−1| = x−10

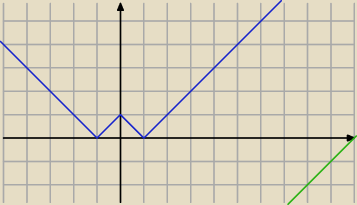
Qulka: brak rozwiązań

astra: A tak niegraficznie jak to by wyglądało? Bo robiąc tak wychodzi mi, że x=5,5 jest jedynym rozw tego równania

getin: |x|−1 = x−10 lub |x|−1 = −x+10 |x| = x−9 lub |x| = −x+11 x=x−9 lub x=−x+9 lub x=−x+11 lub x=x−11 0=−9 lub x=4,5 lub x=5,5 lub 0=−11 sprawdzamy czy rzeczywiście x=4,5 oraz x=5,5 są rozwiązaniami ||4,5|−1| = 4,5−10 |4,5−1| = −5,5 |3,5| = −5,5 więc x=4,5 nie jest rozwiązaniem ||5,5|−1| = 5,5−10 |5,5−1| = −4,5 |4,5| = −4,5 więc x=5,5 też nie jest rozwiązaniem Odp. Równanie sprzeczne, brak rozwiązań

Qulka: tak niegraficznie to z definicji rozpisz

astra: Dziękuję!

kruk: ||x|−1|=x−10 A można tak ? Dla x<10 sprzeczne a dla x≥10 możemy chyba (?) stwierdzic |x|=x oraz |x−1|=x−1 czyli będzie x−1=x−10 sprzeczność . Ma to sens ?

Qulka: można tak

kruk: dzieki