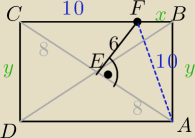
 Z pitagroasa |CF| = 10 oraz |AF| = 10
Niech prostokat ma boki 10+x, y
wtedy 2 razy Pitagoras:
{ (10+x)2 + y2 = 162
{ (x2 + y2 = 102
odejmujac drugie od pierwszego
(10+x)2 − x2 + y2 − y2 = 162 − 102
(100 + 20x + x2) − x2 = 256 − 100
100 + 20x = ...
x = ...
y = ...
No i ostateczny pitagoras
y2 + 102 = |DF|2
Z pitagroasa |CF| = 10 oraz |AF| = 10
Niech prostokat ma boki 10+x, y
wtedy 2 razy Pitagoras:
{ (10+x)2 + y2 = 162
{ (x2 + y2 = 102
odejmujac drugie od pierwszego
(10+x)2 − x2 + y2 − y2 = 162 − 102
(100 + 20x + x2) − x2 = 256 − 100
100 + 20x = ...
x = ...
y = ...
No i ostateczny pitagoras
y2 + 102 = |DF|2
 Robiłem to zadanie trochę pokrętnym sposobem korzystając z podobieństw trójkątów i twierdzenia
kosinusów i |DF| wyszło mi w przybliżeniu 13,86.
Stwierdziłem, że mogę gdzieś mieć błąd więc zrobiłem jeszcze raz używając 2 razy twierdzenia
Pitagorasa i znów |DF| wychodzi mi tak samo
Robiłem to zadanie trochę pokrętnym sposobem korzystając z podobieństw trójkątów i twierdzenia
kosinusów i |DF| wyszło mi w przybliżeniu 13,86.
Stwierdziłem, że mogę gdzieś mieć błąd więc zrobiłem jeszcze raz używając 2 razy twierdzenia
Pitagorasa i znów |DF| wychodzi mi tak samo

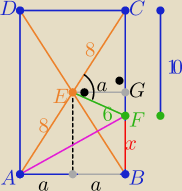
| 8*6 | ||
1/ w ΔCEF : |CF|=10 =|AF| to |EG|=a= | =4,8 ⇒ |AB|=2a=9,6 | |
| 10 |
