trójkąt
Iwka: Niech ABC bedzie trójkątem o największym polu w którym ∡ABC=2∡BAC oraz BC=1.
Oblicz cos∡ABC.
13 cze 21:08
Qulka: 1/2
13 cze 23:18
Iwka: czemu tak?
13 cze 23:31
Qulka: bo największe pole jest wtedy gdy sin =1

13 cze 23:50
Qulka:
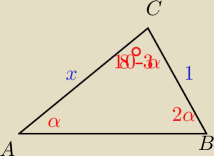
tw. sinusów stabilizuje nam x
Pole P=
12x•1•sin(180−3α) max gdy 180−3α=90 czyli α=30°
cos2α=cos60° = 1/2
13 cze 23:55
Iwka: A ile to pole wynosi ?
13 cze 23:59
Qulka: √3
14 cze 00:04
Qulka: tzn √3/2
14 cze 00:04
Iwka: "bo największe pole jest wtedy gdy sin =1" nie rozumiem tego ?
14 cze 00:13
Qulka: nie no dobra.. też jest x jest funkcją α

tw.sinusów
więc x/2 =cosα
zatem Pole P=cosα•sin(180°−3α) = cosα•sin3α
i tego już mi się nie chciało liczyć

ale może z pochodnych za chwilę ;>
14 cze 00:13
Qulka: P'=cos2α+2cos4α=0
| | √33−1 | |
więc szukany cos2α= |
| |
| | 8 | |
14 cze 00:26

 tw. sinusów stabilizuje nam x
Pole P=12x•1•sin(180−3α) max gdy 180−3α=90 czyli α=30°
cos2α=cos60° = 1/2
tw. sinusów stabilizuje nam x
Pole P=12x•1•sin(180−3α) max gdy 180−3α=90 czyli α=30°
cos2α=cos60° = 1/2
 tw.sinusów
tw.sinusów
 ale może z pochodnych za chwilę ;>
ale może z pochodnych za chwilę ;>