abcd
lisg: W czworokącie wypukłym ABCD połączono kolejno środki boków i otrzymano kwadrat. Zatem:
A. czworokąt ABCD jest kwadratem
B. przekątne czworokąta ABCD przecinają się pod kątem ostrym
C. czworokąt ABCD jest trapezoidem
D. czworokąt ABCD jest deltoidem
Moze być wiecej niz jedna.
13 cze 13:31
Qulka: A,B
13 cze 23:28
an: A,D można rysunek do B
14 cze 12:22
Qulka:
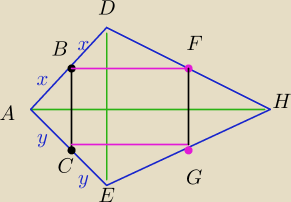
można nawet rysunek do D

ΔABC jest podobny do ΔADE w skali 1/2 więc BC||DE
ΔDBF jest podobny do ΔDAH w skali 1/2 więc BF||AH
skoro kwadrat to BC⊥BF więc DE⊥AH
14 cze 12:37
Qulka: |BC|≠|BF| więc D odpada

14 cze 12:38
bn:
Czy kwadrat jest deltoidem?
14 cze 12:43
Qulka: tak ... każdy kwadrat można zaliczyć do deltoidów ale nie każdy deltoid jest kwadratem
14 cze 12:48
an:
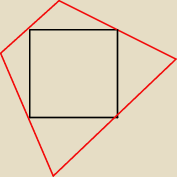
A,C
14 cze 12:52
Qulka: tylko akurat w tym przekątne przecinają się pod kątem prostym...narysuj inny i sprawdz czy też

14 cze 12:54
an: Czy to zabronione
14 cze 12:58
Qulka: nie ale ten przypadek to po prostu B
14 cze 13:02
an: w treści być może źle przepisane
B. przekątne czworokąta ABCD przecinają się pod kątem ostrym
14 cze 13:12
Qulka: aa widziałam tam prostym

po tym jak napisano że kilka

no to tylko A

14 cze 16:05
an: Jest to czworokąt o przekątnych równej długości przecinających się pod kątem prostym,
warunki takie mogą spełnić zgodnie z definicjami figur odpowiedzi A lub C
Czyli przy danych z treści nie można określić odpowiedzi. Może być A lub C nie wiadomo, która
jest
14 cze 22:13
an: Jednak D też
Jest to czworokąt o przekątnych równej długości przecinających się pod kątem prostym,
warunki takie mogą spełnić zgodnie z definicjami figur odpowiedzi A lub C lub D
Czyli przy danych z treści nie można określić odpowiedzi. Może być A lub C lub D nie wiadomo,
która jest
14 cze 22:30
14 cze 22:35
 można nawet rysunek do D
można nawet rysunek do D  ΔABC jest podobny do ΔADE w skali 1/2 więc BC||DE
ΔDBF jest podobny do ΔDAH w skali 1/2 więc BF||AH
skoro kwadrat to BC⊥BF więc DE⊥AH
ΔABC jest podobny do ΔADE w skali 1/2 więc BC||DE
ΔDBF jest podobny do ΔDAH w skali 1/2 więc BF||AH
skoro kwadrat to BC⊥BF więc DE⊥AH

 A,C
A,C

 po tym jak napisano że kilka
po tym jak napisano że kilka  no to tylko A
no to tylko A 