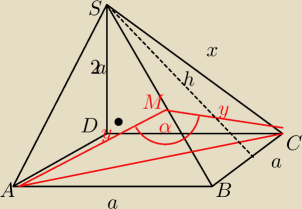
stereometria salamandra: Podstawą ostrosłupa ABCDS jest kwadrat ABCD. Krawędź boczna SD jest wysokością tego ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi ABS i CBS tego ostrosłupa. x=a√5

	1
h2+(		a)2=5a2
	2

	19
h2=		a2
	4

	√19
h=		a
	2

	√19   a* a   2		a2√19
PBCS=		=
	2		4

	y*x
PBCS na drugi sposób:
	2

a2√19		y*a√5
	=
4		2

4y*a√5=2a²√19

	2a2√19		2a√95
4y=		=
	a√5		5

	a√95
y=
	10

Z twierdzenia cosinusów w AMC:

	95		95		a√95		a√95
(a√2)2=		a2+		a2−2*		*		*cosα
	100		100		10		10

	190		190
2a2=		a2−		a2*cosα
	100		100

10		190
	a2=−		a2*cosα
100		100

	1
cosα=−
	19

1
	+sin2α=1
361

	6√10
sinα=
	19

Wskazałby ktoś błąd?

fil: Trojkat SBC jest prostokatny

wredulus_pospolitus:

	y*x
Dlaczego PBCS =
	2

Skoro 'y' (wysokość ściany bocznej) jest poprowadzona wierzchołka C i pada na bok SB |SB| = √4a² + 2a² = √6a

salamandra: myślałem, że SBC równoramienny, więc SB również = x

wredulus_pospolitus: no to się baaaardzo pomyliłeś

salamandra: Skąd fil od razu wiesz, że jest on prostokątny? Później z Pitagorasa faktycznie to wynika

wredulus_pospolitus: skoro DS jest wysokością tego ostrosłupa ... to znaczy że DS jest prostopadła do płaszczyzny podstawy (kwadratu ABCD), więc DS jest prostopadły do KAŻDEJ prostej zawartej w tejże płaszczyźnie ... w tym także do CD

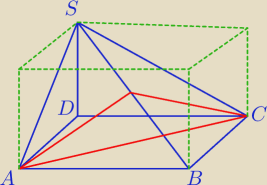Shizzer: Ja również tego zagadnienia do końca nie rozumiałem, ale przeczytałem gdzieś wyjaśnienie, którego autorem była Mila. Pisała kiedyś, w którymś temacie, że na ostrosłupie, którego wysokością jest jedna z jego krawędzi bocznych i podstawą jest prostokąt można opisać prostopadłościan. Mniej więcej tak to było napisane, ale nie pamiętam dosłownie, bo nie mogę tego posta znaleźć W każdym razie rysunek wszystko wyjaśnia. Dzięki temu zrozumiałem dlaczego konkretne trójkąty są prostokątne w przypadku takich ostrosłupów. Może Tobie też się przyda

salamandra: Ja rozumiem, że SDA i SDC prostokątne, nie rozumiałem jedynie skąd fil od razu wie, że SBC będzie prostokątny. Mimo to ładny rysunek, dzięki

Shizzer: Też wiedziałem dlaczego SDA i SDC są prostokątne, ale z tego rysunku zrozumiałem dlaczego SBC i SAB są także prostokątne, ale to już co dla kogo wygodniejsze

Mila: