szescian hania: Dany jest sześcian ABCDEF GH o krawędzi długości 2. Punkt P jest środkiem krawędzi BC . Płaszczyzna AHP przecina krawędź CG w punkcie R (zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty A ,H ,R i P . https://zadania.info/d454/9426084 czy jest ktos w stanie mi pomoc zrozumiec czemu R lezy tez w polowie boku i jestesmy tego pewni? na poczatku sama tak zalozylam i liczylam ale teraz rozmyslam czemu

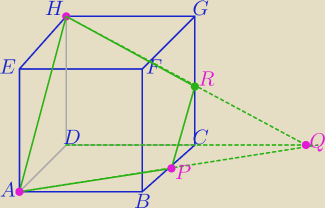
Mila: P jest środkiem BC Zaczynasz rysować przekrój : 1) odcinek AH, 2) Półprosta AP, półprosta DC− otrzymujesz punkt Q 3) odcinek HQ otrzymujesz R PR || AH Jeśli znajdę animację, to dam linka, a może ite pojawi się na forum (zaglądaj), to lepiej wyjaśni , bardziej obrazowo w geogebrze.

hania: dziekuje, ale kurcze nie umiem nadal tego zadania zozumiec, czemu akurat sie napewno przetna w tym jednym punkcie Q i czemu to przez polowe przejdzie,

hania: nwm moze to jest oczywiste ale ja za nic nie moge ogarnac tgo zadania

ite: https://www.geogebra.org/3d/jypdjubk @hania poobracaj myszką ten sześcian, obejrzyj z każdej strony, może to coś wyjaśni. Płaszczyzna wyznaczona przez punkty APH została przecięta dwoma równoległymi (do siebie ale nie do APH) płaszczyznami ADHE i BCGF. Te równoległe płaszczyzny wyznaczyły na APH dwie równoległe proste: AH i PR.

ite: tutaj z zaznaczonym punktem Q https://www.geogebra.org/3d/uddrjqn6

Mila: Dziękuję Pozdrawiam.