wyznaczenie prostej oikodat: A(1,−1) B(5,2) Wyznacz prostą przechodzącą przez A i odległą o 4 od B

ICSP: l : ax + by + c = 0 − równanie prostej a − b + c = 0 ⇒ c = b − a l : ax + by + b − a = 0 d_B,l = 4

	|5a + 2b + b − a|
dB,l =		= 4
	√a2 + b2

itd.

oikodat: |4a+3b|= 4 * sqrt(a²+b²) 16a²+24ab+9b²= 16 a²+16 b² 24 ab−16b²=0 b(3a−2b)=0 b=0 ( oraz a dowolne) lub b=3/2 * a Ale z tego wynika, że jest nieskończenie wiele takich prostych a na zdrowy rozum powinny byc dwie. Gdzie błąd robię ?

ICSP: weź b = 0 Podstaw do równania prostej l Podziel przez a.

	3
Tak samo zrób w przypadku b =		a
	2

ICSP: Druga sprawa: 9b² − 16b² = −7b²

oikodat: dzięki, juz widzę Jakby ktos inny na to patrzył − dostajemy ax−a=0 czyli x−1=0 czyli x=1 oraz x+3/2 * y+1/2 =0

oikodat: wrrr.... oczywiście inna liczba bo bład rachunkowy z b² zzrobiony. tam inny ułamek wyjdzie (nie 3/2 tylko 24/7 zdaje się))

23:

	24
wyjdzie x+		(y+1)−1=0
	7

oikodat: Tak, dokładnie taki wynik. Dla super dokładnych − należy w pewnym miejscu założyć, ze a≠0 by móc dzielić , ale to w tym wypadku jest niezmieniające rozwiązania.

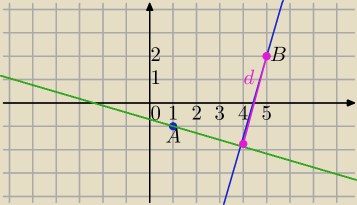
Mila: A(1,−1) B(5,2) k: y=ax+b i A∊k⇔−1=a+b⇔b=−1−a ax−y−1−a=0

	|a*5−2−1−a|
d(B,k)=4⇔		=4
	√a2+1

|4a−3|=4√a²+1 /² 16a²−24a+9=16a²+16 −24a=7

	7
a=−
	24

	7		17
k: y=−		x−		⇔
	24		24

24y=−7x−17 k: 7x+24y+17=0 ============

ICSP: Mila ten sposób nie uwzględnia prostych które nie są funkcjami (prostych pionowych) Dlatego bardziej przepadam za równaniem prostej : Ax + By + C = 0

Mila: Tak, masz rację i dlatego należy sprawdzić odległość B=(5,2) od prostej x=1. Ta odległość jest również równa 4. Czyli: x=1 i 7x+24y+17=0