planimetria
ZWI19: W jakim wielokącie foremnym stosunek miary jednego z kątów zewnętrznych do miary kąta
wewnętrznego jest równy 2:7?
12 cze 16:02
janek191:
Dziewięciokąt foremny.
12 cze 16:08
ZWI19: jak to obliczyć?
13 cze 15:05
a7:
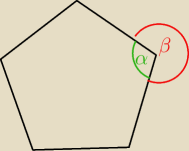
wg moich wyliczeń w pięciokącie foremnym jest 3:7 (stosunek miary kąta wewnętrznego α do
zewnętrznego β), ale 2:7 nie doliczyłam się w żadnym wielokącie foremnym
13 cze 16:46
janek191:
Ma być stosunek miary kata zewnętrznego do miary kąta wewnętrznego !
13 cze 16:57
janek191:
β − to nie jest kąt zewnętrzny
!
13 cze 16:57
janek191:
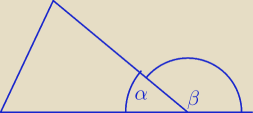
α − miara kąta wewnętrznego
β − miara kąta zewnętrznego
13 cze 17:00
janek191:
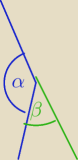
α = 7 x
β = 2 x
7 x + 2 x = 9 x = 180
o
x = 20
o
α = 140
o β = 40
o
n − ilość wierzchołków wielokąta foremnego
Mamy
| | ( n − 2)*180o | |
|
| = 140o / *n |
| | n | |
180
o* n − 360
o = 140
o *n
40
o *n = 360
o / : 40
o
n = 9
====
140
o : 40
o = 7 : 2
13 cze 17:33
janek191:
α = 7 x
β = 2 x
7 x + 2 x = 9 x = 180
o
x = 20
o
α = 140
o β = 40
o
n − ilość wierzchołków wielokąta foremnego
Mamy
| | ( n − 2)*180o | |
|
| = 140o / *n |
| | n | |
180
o* n − 360
o = 140
o *n
40
o *n = 360
o / : 40
o
n = 9
====
140
o : 40
o = 7 : 2
13 cze 17:35
janek191:
α = 7 x
β = 2 x
7 x + 2 x = 9 x = 180
o
x = 20
o
α = 140
o β = 40
o
n − ilość wierzchołków wielokąta foremnego
Mamy
| | ( n − 2)*180o | |
α = |
| = 140o / *n |
| | n | |
180
o* n − 360
o = 140
o *n
40
o *n = 360
o / : 40
o
n = 9
====
140
o : 40
o = 7 : 2
13 cze 17:36
a7: ok, w takim razie wszystko się zgadza, nie wiedziałam, który uznaje się na zewnętrzny, sorki
13 cze 17:41
a7: sorki
13 cze 17:42
a7:
13 cze 17:42
a7: sorki
13 cze 17:42
a7:
13 cze 17:42