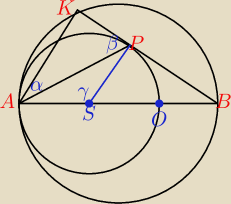
Planimetria - zadanie dowodowe. FUITP: Dwa okręgi o różnych promieniach są styczne wewnętrznie w punkcie A. Odcinek AB jest średnicą większego okręgu, a cięciwa BK tego okręgu jest styczna do mniejszego okręgu w punkcie P. Uzasadnij, że odcinek AP zawiera się w dwusiecznej kąta KAB. Kąt AKP = 90, bo jest to kąt wpisany w okrąg oparty na średnicy. Odcinek KB jest styczny do okręgu o punkcie S, więc kąt KPS = 90. Kąt APS = 90 − β. Trójkąt ASP jest równoramienny więc kąt APS = SAP. 90 − β + 90 − β + γ = 180 ⇒ γ = 2β. W czworokącie ASPK, suma miar wszystkich kątów równa jest 360, więc: 90 + α + 90 − β + 2β + 90 − β = 360 ⇒ α = 90 − β. Kąt SAP = 90 − β, oraz kąt PKA = 90 − β, więc SAP = PKA co kończy dowód. Może tak być?

FUITP: Niepotrzebnie zaznaczyłem punkt O, no i oczywiście punkt S jest środkiem mniejszego okręgu, też mi to uciekło w zapiskach.

Igor Legucki: Może tak być Ale jest prostsza metoda, mianowicie trójkąt APS jest równoramienny dlatego kąt APS = 90−β ,więc kąt PAS = 90 − β. Kąt α wyznaczamy z trójkąta KAB ,czyli 90 + β + α = 180 ⇒ α=90−β A skoro kąt PAS jest równy kątowi α ,to zadanie jest udowodnione

Igor Legucki: Kąt α wyznaczamy z trójkąta KAP*