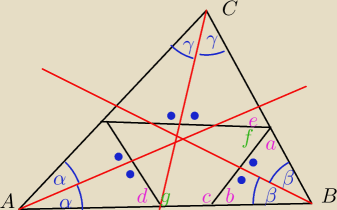
dowód salamandra: Trójkąt ABC jest ostrokątny oraz AC>BC. Dwusieczna d_c kąta ACB przecina bok AB w punkcie K. Punkt L jest obrazem punktu K w symetrii osiowej względem dwusiecznej d_a kąta BAC, punkt M jest obrazem L w symetrii osiowej względem dwusiecznej d_c kąta ACB, a punkt N jest obrazem punktu M w symetrii osiowej względem dwusiecznej d_b kąta ABC. Udowodnij, że na czworokącie KNML można opisać okrąg. kąt d: 180−(90+α)=90−α kąt b: 180−(90+β)=90−β kąt e: 90−γ kąt a: 90−β kąt f: 180−(90−y)−(90−β)=γ+β kąt g: 180−(90−α)=90+α 2γ+2β=180−2α γ+β=90−α Na czworokącie można opisać okrąg wtedy i tylko wtedy, gdy suma przeciwległych kątów jest równa 180. g+f= 180 90+α+90−α=180 180=180 Jest ok?

Poprostupatryk: Jest poprawnie