Pani zadała trudne zadanie może zdam: W trapezie ABCD o podstawach |AB|=2|CD| Punkt S jest środkiem ramienia AD Wiedząc że w czworokąt BCDS można wpisać okrąg Wykaż,że |AB|=|AD|

janek191: Kiedy w czworokąt można wpisać okrąg ?

Eta: @janek191 To nie jest takie "hop− siup"

Eta: No i janek191 .............. poszedł na działkę posadzić warzywka

Eta: Może salamandra się skusi Takie zadanko może być........ na maturce ( i co wtedy ?)

salamandra: A wtedy będzie płacz i zgrzytanie zębów... zaraz spróbuję, o ile siły pozwolą.... od wczoraj ledwo żyję.. a do poniedziałku coraz mniej czasu

Eta: 100% złapałeś i ledwo żyjesz ?

salamandra: ze zmęczenia dzisiaj dwa egzaminy z angielskiego, dużo czekania, siedzenia na sali 2h bezczynnie robią swoje, no i ten przyszły poniedziałek z tylu głowy jeszcze potęguje wszystko..

Eta: Godzina minęła

salamandra: Ja nie dam rady, próbowałem coś z warunku wpisywalności okręgu, nawet z tw. cosinusów coś, ale nic nie idzie, dowody to nie moja mocna strona

Eta: Fajne zadanko

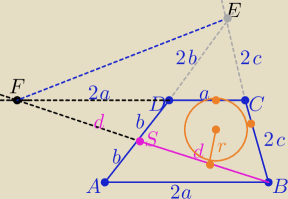
Eta: Nie chce mi się wszystkiego dokładnie opisywać 1/ dorysujmy przedłużenia ramion do punktu E i przedłużenia BS i CD do punktu F 2/ otrzymujemy ΔABS ≡ΔDSF z cechy ( kbk) to FD=AB=2a i SB=SF=d oraz DE=AD=2b i EC=CB=2c ( z Talesa) 3/ Odcinki ES i FC są środkowymi odpowiednio w trójkącie BEF zatem dzielą trójkąt na trójkąty o równych polach ⇒ P(BCF)=P(BSE) 4/ okrąg wpisany w czworokąt BCDS jest też wpisany w trójkąty BCF i BSE a skoro mają one równe pola ,to muszą mieć jednakowe obwody ze wzoru P=r*p teraz już ( łatwiej)zbliżamy się do końca dowodu L(BCF)=2a+a+2c+2d) = L(BSE)=b+2b+2c+2c+d i z warunku wpisania tego okręgu w czworokąt BCDS b+2c=a+d teraz otrzymujemy: a+d+2a+d= b+2c+2b+d ⇒ b+2c+2a+d= b+2c+2b+d⇒ 2a=2b i mamy tezę: |AB|=|AD| ======== ładne zadanie

salamandra: szacun..