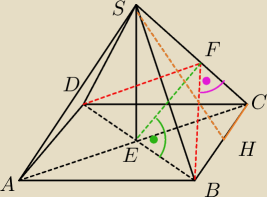
planimetria Poprostupatryk: Proszę o pomoc. W ostrosłupie prawidłowym czworokątnym ABCDS o podstawie ABCD wysokość jest równa h, a kąt między sąsiednimi ścianami bocznymi ostrosłupa wynosi α. Oblicz objętość tego ostrosłupa Prosta BF zawsze będzie pod kątem prostym do SC prawda? Nie wydaje mi się, że w każdym przypadku tak jest, ale pan z https://www.youtube.com/watch?v=FDpZX9kWtFY tak mówi więc na tym opierałem swoje rozwiązanie. Podam zaraz moje rozwiązanie

Poprostupatryk: Już wiem. Ta płaszczyzna DBF zawsze będzie pod katem prostym do SC. Podaję swoje rozwiązanie ΔBFE Twierdzenie Pitagorasa: |SF|² + |SB|² = |FB|² ΔESH Twierdzenie Pitagorasa:

	a		a2
h2 + (		)2 = |SH|2 ⇒ |SH|=√h2 +		(1)
	2		4

ΔSHS ~ ΔBFC

|SC|		a		|SH| * a
	=		⇒ |BF| =		(2)
|SH|		|BF|		|SC|

ΔSCE Twierdzenie Pitagorasa"

	a2		a2
h2+		= |SC|2 ⇒ |SC| = √h2 +		(3)
	2		2

w (2) podstawiam (1) i (3)

	a2   √h2 + * a   4
|BF| =
	a2   √h2 +   2

	α		a√2
sin		=
	2		2|BF|

Czy do tego miejsca są jakieś błędy?

ite: ΔBFE Twierdzenie Pitagorasa: |SF|² + |SB|² = |FB|² ← ↖ nie wiadomo o który trójkąt chodzi

Poprostupatryk: O faktycznie, przepraszam |EF|² + |EB|² = |FB|²

fil: A co to za trojkat SHS?

Poprostupatryk: Chodziło mi o ΔSHC, są takie pomyłki bo przepisywałem z zeszytu gdzie miałem dwa wierzchołki zaznaczone na odwrót

ite: nie ma błędów