kwadrat pulse: Dany jest prostokąt ABCD. Niech E∊BC ,F∊DC tak że ∡DAF = ∡ FAE. Uzasadnij że jęśli DF + BE = AE to ABCD jest kwadratem.

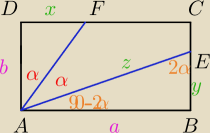
Qulka: jeśli x+y=z to a=b cos2α=y/z −> y=z•cos2α sin2α=a/z −> z=a/sin2α tgα=x/b −> x=b•tgα b•tgα + z•cos2α =z

	a		2sin2α
b•tgα= z(1−cos2α) =		•(1−1+2sin2α) = a•		=a•tgα
	sin2α		2sinαcosα

b=a

herm32: nie rozumiem tego założenia, że x+y=z. Wytłumaczy ktoś?

Qulka: wynika z warunków zadania