zbiór rozwiązań równania GoldeN: Cześć, mam zdanie i nie wiem co robię w nim źle: Wskaż zbiór wszystkich roziwązań równania |cos(a)+cos(3a)+cos(5a)|=3 i robię: cos a = 1 v cos a=−1 cos 3a = 1 v cos 3a=−1 cos 5a = 1 v cos 5a=−1 wtedy: a = 2kPI v a = PI + 2kPI a= 2kPI/3 v a = PI/3 + 2kPI/3 a = 2kPI/5 v a = PI/5 + 2kPI/5 Poprawne rozwiązanie to: a = n x 180*, n jest dowolną liczbą całkowitą

Jerzy: Albo każy cos jest równy 1, albo każdy −1

GoldeN: Czyli tak jak rozpisałem. Jednak moje rozwiązanie nie zgadza się z odpowiedzią

Jerzy: Źle rozpisałeś.

GoldeN: Mógłbyś wyjaśnić w takim razie jak zrobić to poprawnie?

Jerzy: Masz trzy alternatywy, a musisz mieć alternatywę dwóch koniunkcji.

GoldeN: Wychodziłem z cosa + cos3a + cos 5a = 3 v cosa + cos3a + cos5a = −3 i wtedy każdy z nich musi być dla Lewej równy 1 a dla prawej −1

ABC: czyli musisz zapisać (cosa=1 i cos3a=1 i cos5a=1) lub (cosa=−1 i cos3a=−1 i cos5a=−1)

GoldeN: Kurcze tak miałem zrobione od początku jednak nie spiąłem klamerką każdej ze stron. Mój błąd w zapisie. Okej, ale w takim razie co zrobić dalej żeby osiągnąć szukany wyniki?

Jerzy: Licz po kolei każdy z warunków.

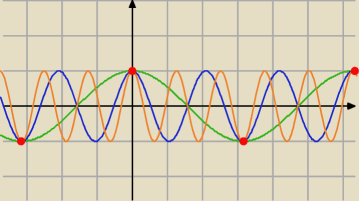
a7: zielony kolor cosa, niebieski cos3a, pomarańczowy cos5a, rozwiązania są co π (wszystkie sa równe jeden co 2π, oraz wszytskie są naraz równe minus jeden co dwa π) czyli odpowiedź będzie kπ, gdzie k jest liczbą całkowitą, inaczej n*180

a7: (poprawka minus jeden też co 2π) czyli w sumie co π

GoldeN: Teraz zrozumiałem że liczą się tylko punkty w których zbiegają się wszystkie trzy wykresy. Zapomniałem o działaniu klamerki jako "i". Dzięki bardzo za pomoc

Jerzy: