dowód jarek: Matura Pokaż że w trapezie ABCD gdzie K przeciecie przekatnych mamy:

AK*CK		BK*DK
	=
AC2		BD2

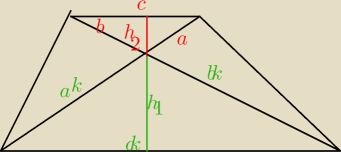23: Trojakty podobne z czerwona wysokością i zieloną wysokością : niech skala k=U{h₁]{h₂} Wtedy podstawiasz do podanej zaleznosci i masz:

a2k		bk
	=		i teraz dzielisz jeden ułamek przez a2 licznik i mianownik,
(ak+a)2		bk+b

analogicznie dugi przez b²

k		k
	=
k+1		k+1

23: troche pogubiłem oznaczenia i literki.... ale taka idea doprowadzi cię do rozwiązania

Mila:

AK*CK		BK*DK
	=
AC2		BD2

	b
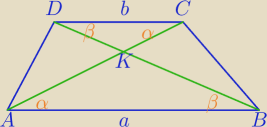
ΔDCK∼ΔABK cecha kkk skala podobieństwa k=		⇔
	a

	b
1) |CK|=		|AK|
	a

	b
|DK|=		*|BK|
	a

	b		b		a+b
2) |AC|=|CK|+|AK|=		|AK|+|AK|=|AK|*(		+1)=|AK|*
	a		a		a

	a+b
|BD|=|BK|+|DK| =|BK|*
	a

3)

	AK*CK		b   |AK2*   a
L=		=		=
	AC2		a+b   |AK|2*( ))2   a

	b		a2
=		*		⇔
	a		(a+b)2

	ab
L=
	(a+b)2

	BK*DK		b   |BK|2*   a
P=		=		⇔
	BD2		a+b   |BK|2*( )2   a

	ab
P=
	(a+b)2

L=P =====

Eta:

	ab
1/ Odcinki |EK|=|FK|= x −− są równej długości x=
	a+b

2/ z podobieństwa trójkątów z cechy (kkk) CKF i ABC oraz EKD i ABC oraz ABK i CDK to:

	CK		x		DK		AK		BK
		=		=		i		=
	AC		a		BD		AC		BD

mnożąc stronami otrzymujemy tezę

|AK|*|CK|		|CK|*|DK|
	=
|AC|2		|BD|2

=================