równanie Marta: Niech a,b,c rzeczywiste oraz a ≠ 0. Ponadto załóżmy że liczba a oraz liczba 4a+3b+2c są tego samego znaku. Wykaż że ax²+bx+c=0 nie może mieć pierwiastków w przedzile (1,2).

wredulus_pospolitus: Trudno udowodnić coś co nie musi być prawdą: (x−1.1)(x+100) = 0 x² + 98.9x − 110 = 0 a = 1 > 0 4a + 3b + 2c = 4 + 296,7 − 220 = 80,7 > 0 A pierwiastek posiada

Marta: Tu chodzi że obu pierwiastków.

Marta: Sorry za nieścisłość.

Marta: Już wiem idzie z wzorów Vieta

23: Marta pokaż jak bo jestem ciekaw

Marta: Wzory Vieta a potem wyciaganie przed nawias, spróbuj

23: Tak sobie myśkę, jeśli oba byłyby z przedziału 1<x₁<2 i 1<x₂<2 to po dodaniu wyszłoby, że 2<x₁+x₂<4 to czy nie wystarczy pokazać, że x₁+x₂≥4 lub x₁+x₂≤2 ?

Chorus : 23, skąd wziąłeś ≥ ≤ ?

23: Chorus a jak powinno byc ?

getin: 1<x₁<2 i 1<x₂<2 nie jest równoznaczne z 2<x₁+x₂<4 np. x₁ = 0 i x₂ = 3 nie spełnia jednocześnie 1<x₁<2 i 1<x₂<2 a spełnia 2<x₁+x₂<4

23: getin to jaki masz pomysł bo ciekawi mnie rozwiązanie. Może f(1) i f(2) wyznaczyć i spróbować pokazac ze są jednakowych znaków ?

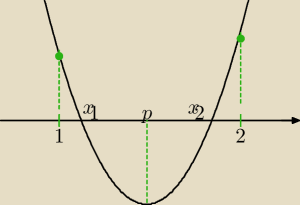
getin: ja bym to podzielił na dwa przypadki: pierwszy dla a>0 i drugi dla a<0 zakładamy przeciwnie, że oba pierwiastki należą do przedziału (1, 2), tzn. 1<x₁<2 i 1<x₂<2 z tego wynika że 2<x₁+x₂<4 i 1<x₁*x₂<4 1^o: układ nierówności {a>0 {2<x₁+x₂<4 {1<x₁*x₂<4 {1<p<2 {4a+3b+2c > 0 (z założenia) {Δ > 0 pierwszy warunek a>0 pomijamy udowodnimy że rozwiązaniem układu nierówności {2<x₁+x₂<4 {1<x₁*x₂<4 {1<p<2 {4a+3b+2c > 0 {Δ > 0 jest zbiór pusty, więc nałożenie dodatkowego warunku a>0 spowoduje że tym bardziej wyjdzie zbiór pusty

	x1+x2
ponieważ p =		, to nierówność 2<x1+x2<4 jest równoważna 1<p<2
	2

pomijamy więc 1<p<2 zostaje {2<x₁+x₂<4 {1<x₁*x₂<4 {4a+3b+2c > 0 {b²−4ac > 0 trzecią nierówność dzielimy stronami przez (dodatnie) a czwartą nierówność dzielimy przez a² {2<x₁+x₂<4 {1<x₁*x₂<4

	b		c
{4+3		+2		> 0
	a		a

	b2		a*c
{		−4		> 0
	a2		a2

wykorzystujemy wzory Viete'a {2<x₁+x₂<4 {1<x₁*x₂<4 {4−3(x₁+x₂)+2x₁*x₂ > 0 {(x₁+x₂)²−4x₁*x₂ > 0 dla ułatwienia podstawiamy x₁+x₂ = x x₁*x₂ = y {2<x<4 {1<y<4 {4−3x+2y>0 {x²−4y>0 {2<x<4 {1<y<4

	3
{y>		x−2
	2

	1
{y<		x2
	4

rysujemy to w układzie współrzędnych 2<x<4 to obszar między prostymi x=2 i x=4 1<y<4 to obszar między prostymi y=1 i y=4

	3		3
y>		x−2 to obszar powyżej prostej y=		x−2
	2		2

	1		1
y<		x2 to obszar poniżej paraboli y=		x2
	4		4

te 4 powyższe obszary nie mają części wspólnej więc nie istnieją x₁ i x₂ żeby każdy z nich należał do przedziału (1,2) drugi przypadek: dla a<0 bardzo podobnie rozważamy pamiętamy że przy dzieleniu nierówności przez ujemne a zmieniamy znak nierówności

Marta: a(4a+3b+2c)>0 4+3b/a+2c/a>0 Niech pierwiastki to k i l 4−3(k+l)+2kl>0 (1−k)(2−l)+(2−k)(1−l)>0 Gdyby k,l∈(1,2) wtedy musiało by być (1−k)(2−l)+(2−k)(1−l)<0.

23: Getin ale pisałeś ze to nie jest równoważne i podałeś liczy 0 i 3 a potem z tego korzystasz to jak to jest ?

getin: bo z 1<x₁<2 i 1<x₂<2 nie wynika samo 2<x₁+x₂<4 tylko z 1<x₁<2 i 1<x₂<2 wynika 2<x₁+x₂<4 i 1<x₁*x₂<4

23: Rozumiem. Dzieki

getin: możesz sobie to wyobrazić że x₁ = x oraz x₂ = y 1<x₁<2 i 1<x₂<2 czyli 1<x<2 i 1<y<2 zatem odpowiednikiem warunków 1<x<2 i 1<y<2 jest obszar wspólny pasa między liniami x=1 i x=2 oraz pasa między liniami y=1 i y=2 ten obszar wspólny to kwadrat o wierzchołkach (1,1), (1,2), (2,2) i (2,1) patrzymy na lewy dolny wierzchołek (1,1) i prawy górny wierzchołek (2,2) wobec tego suma x+y zawiera się między 2 a 4 zaś iloczyn x*y przyjmuje wartości z przedziału od 1 do 4

23: A jak wezme x1=0,5 x2=3 to nie zajdzue od konca tzn2< x1+x2 <3 oraz 1<x1x2<4 a nie zajdzie 1<x1<2

23: Powinno być wyżej x₁=0,5 oraz x₂=3 wtedy 2<x₁+x₂<4 i 1<x₁x₂<4 ale już nie spełnia warunków 1<x₁<2 i 1<x₂<2

23: To jak to jest?

getin: wynikanie p⇒q jest fałszywe gdy poprzednik jest prawdziwy (p=1) a następnik fałszywy (q=0) w pozostałych trzech przypadkach jest prawdziwe p | q | p⇒q | −−−−−−−−−−−−−−−− 1 | 1 | 1 1 | 0 | 0 0 | 1 | 1 0 | 0 | 1 poprzednik czyli p wygląda tak: 1<x₁<2 i 1<x₂<2 następnik czyli q jest taki: 2<x₁+x₂<4 i 1<x₁*x₂<4 dla x₁=0,5 i x₂=3 poprzednik jest fałszywy (p=0) 1<0,5<2 i 1<3<2 a następnik jest prawdziwy (q=1) 2<3,5<4 i 1<1,5<4 dla x₁=0,5 i x₂=3 mamy wartości logiczne p=0, q=1 więc wynikanie p⇒q jest prawdziwe (1)

Marta: A moje rozwiązanie wam nie wystarczy?

23: Ale miales pokazać rowowaznosc swoich warunków a nie implikacje

23: Marta chciałem tylko zrozumieć dlaczego nie mogę wziac jednego warunku do dowodu . Twoje jest ok. Muszę przemyśleć na spokojnie wywód getina że zrobiłam błąd .