Proszę o pomoc xxx1212: 3. W trapez równoramienny ABCD wpisano koło o środku w punkcie O; punkty E i F są punktami styczności tego koła odpowiednio z ramieniem BC i podstawą DC tego trapezu. Wiedząc, że pole tego trapezu jest równe 156 cm2, a ramię BC ma długość 13 cm, oblicz: a) długość wysokości trapezu; b) pole koła wpisanego w trapez; c) pole czworokąta OECF.

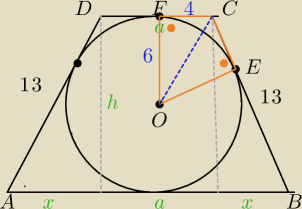
a7: 2a+2x=13+13 a+x=13

	26
156=		*h czyli h=12 x=5 (z tw. Pitagorasa) a=13−5=8 r=h/2=6
	2

A)h=12 (cm) B) πr²=36π (cm²)

	1
C) POECF=2*		*4*6=24 (cm2)
	2

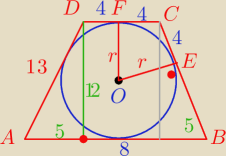
janek191: a) a + b = 2*13 = 26

	a + b		26
P =		*h =		*h = 13 h = 156
	2		2

⇒ h = 12 ========= h = 2 r = 12 r = 6 ===== b) P_k = π r² = 36 π ================== c) P_cz =4 r = 4*6 = 24