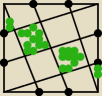
 Każdy bok kwadratu o boku a dzielmy na trzy równe częsi i prowadzimy odcinki tak jak na
rysunku. Oblicz stosunek sumy pol zielionych figur (dwa czworokąty i dwa trójkaty) do pola
kwadratu.
Każdy bok kwadratu o boku a dzielmy na trzy równe częsi i prowadzimy odcinki tak jak na
rysunku. Oblicz stosunek sumy pol zielionych figur (dwa czworokąty i dwa trójkaty) do pola
kwadratu.
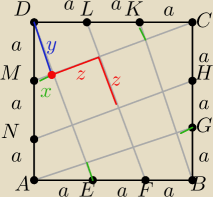 MC=AG=NH=DE=LF=KB=a√10
małe trójkąty prostokątne o przeciwprostokątnych MD AE KC GB są podobne do Δ np. MDC
MC=AG=NH=DE=LF=KB=a√10
małe trójkąty prostokątne o przeciwprostokątnych MD AE KC GB są podobne do Δ np. MDC
| MC | a | a√10 | ||||
dlatego | ={MD}{x} czyli x= | = | ||||
| MD | √10 | 10 |
| 3a√10 | ||
z tw. Piatagorasa y= | ||
| 10 |
| MC−x−y | 3a√10 | |||
z= | = | |||
| 2 | 10 |
| 3a√10 | a√10 | 3a√10 | 21a2 | |||||
PZIELONYCH FIGUR=z2+z2+xy=2*( | )2+ | * | = | |||||
| 10 | 10 | 10 | 10 |
| PZIELONYCH FIGUR | 7 | ||
= | |||
| PKWADRATU ABCD | 30 |
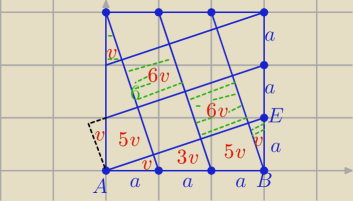 Z podobieństwa trójkątów ( w ΔABE)
mamy pola : v, 3v, 5v
to 6v=a2
P□=9a2= 54v
Pzielonych części=6v+6v+2v= 14v
Z podobieństwa trójkątów ( w ΔABE)
mamy pola : v, 3v, 5v
to 6v=a2
P□=9a2= 54v
Pzielonych części=6v+6v+2v= 14v
| 14v | 7 | ||
= | |||
| 54v | 27 |
 6v −− pole zielonego kwadrat , v −− pole zielonego trójkąta
P□= 2*10v+2*20v = 60v
6v −− pole zielonego kwadrat , v −− pole zielonego trójkąta
P□= 2*10v+2*20v = 60v
| 14v | 7 | ||
= | |||
| 60v | 30 |





