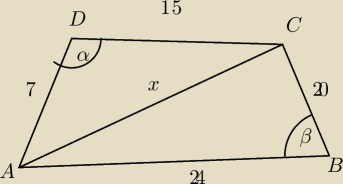
planimetria salamandra: Czworokąt ABCD o bokach długości AB=24, BC=20, CD=15 i AD=7 wpisano w okrąg. Oblicz długość przekątnej AC tego czworokąta. z Tw. cosinusów: x²=49+225−2*7*15*cos(180−β) x²=20²+24²−2*20*24*cosβ x²=274+210cosβ x²=400+576−960cosβ 274+210cosβ=976−960cosβ

	3
702=1170cosβ ⇒ cosβ=
	5

	3
x2=274+210*		=400
	5

x=20 Jest ok takie rozwiązanie?

Qulka: tak ładne że ok

jaros: Jak zamieniłeś α na (180−β) ?

salamandra: α+β=180

jaros: A ok, dziękuję

salamandra: Wiesz skąd to wynika natomiast?

jaros: No tam suma przeciwległych kątów w czworokącie jest równa 180, dobrze mówię?

salamandra: no tam coś dobrze Jeżeli czworokąt jest wpisany w okrąg to suma miar kątów leżących naprzeciwko siebie wynosi 180

kyrtap: sinus cosinus daj Boże 3−