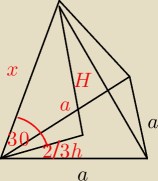
Objętość ostrosłupa prawidłowego trójkątnego jest równa 6p{3} Lukasz: Objętość ostrosłupa prawidłowego trójkątnego jest równa 6√3 a kąt nachylenia krawędzi bocznej do podstawy wynosi 30 stopni. Oblicz dł krawedzi bocznych Hej. Ogólnie znam rozw. tego zadania, ale nie wiem dlllaczego moja metoda nie działa. Pewnie gdzieś mam jakiś głłupi błąd (jak zwykle) i nie moge go znaleźć. H−wys. ostrosłupa h−wys podstawy x−krawedz boczna V = 6√3 6√3 = H * a²√3 / 4 ⇒ H = 6√3 / a²√3 / 4 ⇒ H = 24/a² 2/3h = ap³/2 * 2/3 = a√3/3 Teraz podstawiam dane pod tangens 30: tg30 = H / 2/3h √3/3 = 24/a² / a√3/3 √3/3 = 24*3 / a³√3 3a³ = 24*9 a³ = 72 a= ³√72 Wyliczam H = 24/a² ⇒ H = 2 / ³√3 Podstawiam teraz pod sinus 30 żeby wyliczyć krawędź (x) sin30 = H/x 1/2 = 2/³√3 / x x=4/³√3 Poprawna odp dla x to 4

Lukasz:

Lukasz: Ktoś pomoże ?

a7: to jest ostrosłup to ma inny wzór na objętość 1/3 P_p*H

a7: a³=216 a=6 H=2 x=4

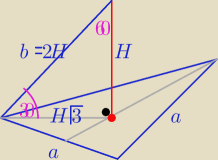
Eta: Na rys. oznaczenia z trójkąta "ekierki" o kątach 30^o,60^o,90^o

	a√3		a
H√3=		⇒ H=
	3		3

	1
V=		Pp*H= 6√3
	3

1		a2√3		a
	*		*		= 6√3 ⇒a3=216 ⇒ a=6
3		4		3

to H=2 i b=2H=4 b=4 ======

Lukasz: Dzięki, nie wiem czemu podstawiałem cały czas pod wzór na graniastosłup. Dzięki