vektory jaros: Dane są wektory BA = [−8;−5] i CA[−8;−11]. Wyznacz współrzędne wektora BC i oblicz cosinus kąta ABC. O co tutaj konkretnie chodzi?

fil: Masz wyznaczyc wspolrzedne vectora BC

ICSP: Chodzi o wyznaczenie współrzędnych wektora BC a następnie obliczenie cosinusa kąta ABC

23: BC= BA+AC =[−8;−5]+[8,11]=[0,6]

fil: Mozesz to zrobic poprzez dodawanie vectorow, ale tez tak: BA=[−8,−5] CA=[−8,−11] x_a−x_b=−8 x_a−x_c=−8 (odejmujesz pierwszego rownania drugie) x_c−x_b=0 y_a−y_b=−5 y_a−y_c=−11(odejmujesz pierwszego rownania drugie) y_c−y_b=6 BC=[0,6]

jaros: BC= BA+AC? to jest jakaś własność?

jaros: No w porządku, mam wektory ale jak z sektorów wyznaczyć punkty ABC?

23: Możesz też narysować i odczytać

23: Jaros wektor BC możesz odczytać jako metode jak przejsc od B do C np. BC=[2,3] odczytać możesz jako 2 prawo i 3 w gorę

jaros: no ale problem jest taki, że to nie są punkty tylko wektory, w takimi razie od czego mam zacząć?

23: Wiec jesli wiesz jak przejsc z B do A a nastepnie z A do C to wiesz jak przejsc z B do C czyli masz wektor BC

23: Narysuj to sobie zacznij od dowolnego punktu i narusyj wektory

23: złączą się one w punkcie A.

23: pokazać Ci to na rysunku ?

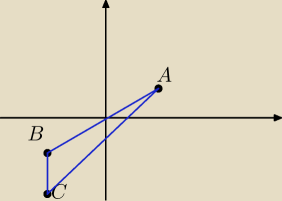
jaros: Sekundke chyba mam, tak?

jaros: Ajć na odwrót

jaros:

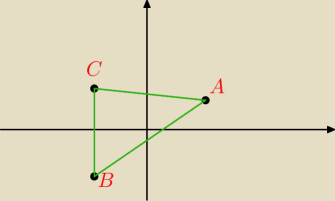
jaros: Nie nie wiem, jak ma być, która literka gdzie

ICSP: BA = [−8;−5] −> idąc od punktu B do punktu A musisz przejść 8 jednostek w lewo oraz 5 jednostek w dół. Twój rysunek kompletnie tego nie obrazuje.

23: coś jest nie tak

jaros: No ktoś wie, gdzie jest błąd?

23: https://zapodaj.net/99821ee88ffc5.jpg.html

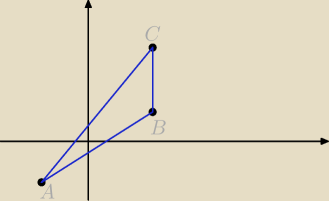
jaros: Dobrze chyba jest git, ktoś wie co i jak z tym kątem?

jaros: A i teraz po prostu tw cos?

ICSP: wzór na sosinus kąta wykorzystujący iloczyn skalarny.

jaros: czyli nie przejdzie tw. cos?

23:

	8
albo tg(180−α)=
	5

ICSP: Licz z twierdzenia cos. Masz dane współrzędne wektorów. Wyliczenie iloczynu skalarnego i długości wektorów to 15s roboty. Jednak upierasz się na tym tw. cosinusów więc licz z niego i z 30s zrób 5 min.

jaros: No ale pokazał byś mi zastosowanie tego iloczynu i po 2 jest błąd w obliczeniach bo bok ma być [0;5]

jaros: znaczy rektor BC

jaros: A dobra ja źle przepisałem, jednak vektor jest dobrze

ICSP: BA = [−8;−5] , BC = [0;6]

	<BC , BA>		−8*0 − 5*6
cos(<ABC) =		=		= ...
	||BC|| ||BA||		√82+52 * √02 + 62

jaros: oki zrobione

jaros: dziękuję pięknie