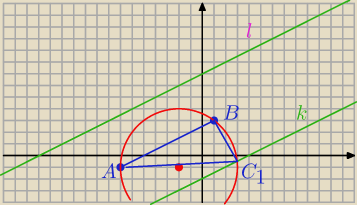
W trójkącie ABC Czarniecki: W trójkącie ABC o polu 20 dane sa współrzędne dwóch wierzchołków: A = (− 7,− 1) , B = (1,3) oraz środek S = (− 2,− 1) okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka C Wyliczyłem, że prosta na której leży C: y=1/2x−5/2 lub y=1/2x+15/2 Ale jak podstawiam współrzędne punktu C do CS²=R², to mi wychodzą wyniki niezgodne z odpowiedzią.

Jerzy: A jak doszedłeś do tych dwóch równań prostych zawierających C ?

janek191: → AB = [ 8, 4 ] I AB I = √64 + 16 = √80 = √16*5 = 4 √5 0,5*4√5*h = 20 h = 2√5 k : y = 0,5 x + 2, 5 − 2√5 ========================= Dokończ

Jerzy: Tutaj masz rozwiązanie: https://zadania.info/d392/2770019

janek191: pr.AB y = 0,5 x + 2,5 0,5 x − y + 2,5 = 0 k : 0,5 x − y + c = 0 I 2,5 − c I = 2√5 więc c = 2,5 − 2√5 lub c = 2,5 + 2√5 k : 0,5 x − y + 2,5 − 2√5 y = 0,5 x + 2,5 − 2√5 ====================== l: y = 0,5 x +2,5 + 2√5

salamandra: Mam pytanie czy gdyby był to trójkąt równoramienny, to można by wyznaczyć prostą SC prostopadłą do AB i z odległości SC równej promieniowi wyznaczyć współrzędne C?

Czarniecki: Salamandra, tak. Wyznaczyłbyś środek odcinka AB i równanie prostej, która przechodzi przez środek AB i punkt S. Dzięki wszystkim