parametr m misio: Jakie warunki podać w zadaniu?

	1		1
Dane jest równanie x2+(2m+1)x−3m2−		m +		=0. Wyznacz zbiór wszystkich wartości
	2		4

parametru m, dla których to równanie ma dokładnie dwa różne rozwiązania mniejsze od 4. W odpowiedziach podali tak Δ>0 no to rozumiem f(4)>0 tego nie rozumiem do końca dlaczego oraz jeszcze jakieś x_w<4, co to jest to x_w. Może ktoś pomóc?

fil: bardzo dobrze podali

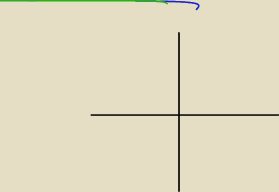
fil: f(4) > 0 przy a > 0 i Δ > 0 daje ci dwie mozliwosci

fil: aha

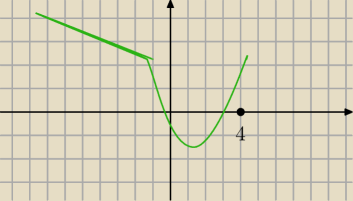
Jerzy: x_w , to odcieta wierzcholka paraboli. Popatrz teraz na rysunek, widzisz dlaczego takie watunki ?

Chorus : Dzięki f(4)>0 xw<4 mamy pewność że x2 znajdujące się między nimi jest mniejsze od 4, tak? Tak w ogóle, w tym przypadku mamy pewność że a ≠ 0 , czy trzeba to koniecznie napisać egzaminatorowi?

fil: w tym przpadku a = 1

misio:

	1		1
czyli xw to −3m2−		m+		?
	2		4

jeszczenie rozumiem tego f(4)>0 nigdy nie spotkałem się z takimi warunkami dlatego pytam

misio: Dlaczego jest f(4)<0 a w zadaniu jest mowa, że oba pierwiastki są mniejsze od 4?

Chorus : miejsce zerowe ma być mniejsze od 4

misio: i nie mogę zrobić tego RĘCZNIE? W sensie, że zapiszę x1 i x2 i po kolei napiszę, że większe od 4? Bo tak zrobiłem i wyszło mi źle

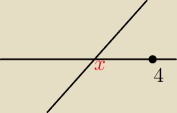
Jerzy: Gdyby w tym zadaniu f(4) byłoby ujemme i x_w < 4, to jeden z pierwiastków byłby większy od 4 (patrz rysunek)

Chorus :

misio: Czyli to x_w to jest to równanie kwadratowe co napisałem wyżej?

Chorus : argument dla wierzchołka

Jerzy: x_w do współrzędna x wierzchołka paraboli.

misio: Dzięki, już rozumiem. Ale dlaczego wybranie warunków: x₁<4 x₂<4 Δ>0 jest gorszym pomysłem? Niepełne są te warunki?

fil: Ze wzgledu na obliczenia

misio: Mam jeszcze pytanie. Bo dosłownie teraz dowiedziałem się o takich warunkach. Macie może jeszcze inne przykłady zadań z parametrem gdzie są jakieś podobne, nietypowe warunki do zadania?

Jerzy: A gdzie widzisz nietypowe warunki w tym zadaniu ?

Jerzy: Masz: Dla jakiego a funkcja y = −x² + a przyjmuje tylko wartości dodatnie.

misio: dla a>x²

ICSP: Δ < 0

misio: A no tak, żeby nie było miejsc zerowych. To wszystkie warunki?

ICSP: to teraz ja: Podać warunki na to aby wielomian w(x) = ax² + bx + c miał dwa pierwiastki takie, że jeden należy do przedziału (d ; e) a drugi należy do przedziału (f ; g) gdzie te przedziały są rozłączne.

Jerzy: @ICSP, to chyba żart.

ICSP: aa tam jest minus ^^ no to lim_{x → ∞} f(x) = −∞ więc ta funkcja nigdy nie przyjmie wartości dodatnich ^^

ICSP: tylko dodatnich*

Jerzy: @ICSP, pytanie dotyczyło wpisu 21:41. Takie a nie istnieje.

Jerzy: Ano właśnie.

ICSP: Już naprawiłem o 21:35

Jerzy: Skup się @misio , y = −x² + a nigdy nie będzie przyjmowała tylko wartości dodatnich.

misio: No trochę mnie zmyliło, bo ramiona paraboli są w dół, dlatego m musiałoby być większe od x², m∊∅ Proszę o jeszcze jakieś fajne. Bo ja znam tylko takie zadanie gdzie trzeba dać, że Δ>0 x₁x₂>0 x₁+x₂>0

Jerzy: A kiedy y = x² + a przyjmuje tylko wartości ujemne ?

misio: Nie przyjmuje nigdy tylko wartości ujemnych. Bo lim_x→∞ f(x)=+∞

misio:

misio: Przepraszam, ale jakie warun ki miałaby funkcja podana w temacie, jeżeli a < 0 Wyznacz zbiór wszystkich wartości parametru m, dla których to równanie f(x) = ax²+bx+c ma dokładnie dwa różne rozwiązania większe od 4 nie byłoby takich chyba bo a<0 i jak tu dać warunek, że f(4)<0 f(4)>0

ICSP: narysuj sobie przykładową funkcję która spełnia twoje wytyczne i spróbuj samodzielnie wyznaczyć warunki. To nie jest trudne.

Szkolniak: (x₁>4 ∧ x₂>4) ⇔ (x₁−4>0 ∧ x₂−4>0) ⇔ ( (x₁−4)(x₂−4)>0 ∧ x₁−4+x₂−4>0 ) ⇔ ⇔ ( x₁x₂−4(x₁+x₂)+16>0 ∧ (x₁+x₂)−8>0) + wzory Viete'a

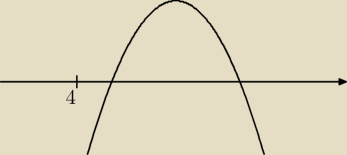
misio: ICSP warunki o których pomyślałem dla takiej funkcji to: Δ>0 x_w>4 y_w>0 f(4) tego raczej nie mogę użyć @Szkolniak bardzo fajnie rozpisane. Nawet nie pomyślałem, że można tak rozpisać ten 3 nawias z 2 nawiasu, pomysłowe.

Szkolniak: Ja w zadaniach tego typu zawsze korzystam z tego co napisałem − dosyć łatwo i szybko się to nawet rozpisuje i wyprowadza, więc bez problemu Nie trzeba też wtedy martwić się o ujemność czy dodatniość współczynnika przy 'x²', w przeciwieństwie właśnie do takiej graficznej metody, gdzie warunki trzeba ułożyć odpowiednio do znaku.

misio: Masz może jakieś fajne trudne zadania żebym sobie mógł to przećwiczyć? Bardzo proszę

Szkolniak: Z takim właśnie poleceniem − większe lub mniejsze od danej liczby czy ogólnie kwadratowe z parametrem?

misio: Może być jedno takie wieksze/mniejsze i jak masz jakieś trudne to poproszę. Ja tylko rozwiązywałem gdy w zadaniu było...„oba pierwiastki dodatnie”. Chodzi mi o to żeby poćwiczyć sobie te warunki w zadaniu, bo dzisiaj się dowiedziałem o takim jak mówicie a zaraz matura// Jak możesz to podaj, zrobię je jutro z rana bo muszę już iść spać.

Szkolniak: Nie wiem jakie są dla Ciebie trudne, ale może takie: 1) Dla jakich wartości parametru m równanie mx²+2x+m−2=0 ma dwa różne pierwiastki mniejsze od 1? 2) Dla jakich wartości parametru m równanie x⁴+mx²+1=0 ma cztery różne pierwiastki? 3) Dla jakich wartości parametru m równanie x²−2m|x|+3m−2=0 ma dwa różne pierwiastki rzeczywiste?

misio: 1) Jeżeli a>0, to warunki: f(1)>0 x_w<1 Δ>0 Wychodzi m ∊ ( 0 ; 1 + √2 ) Jeżeli a<0, to warunki: f(1)<0 x_w<1 Δ>0 Wychodzi m ∊ ∅ więc odpowiedź m ∊ ( 0 ; 1 + √2 )

Jerzy: Merytorycznie jest OK. Rachunkowo nie liczyłem.

misio: W desmosie mi pokazuje okej, jak wpisywałem np za m 0.01 albo 1+√2. Teraz 2) x⁴+mx²+1 = 0 4 rozwiązania x²=t ; t ≥ 0 t²+mt+1 = 0 Δ_t=m²−4 Warunki: hmm no tu mam trochę problem Δ_t > 0 m∊( −∞ ; −2 ) ∪ ( 2 ; ∞ ) t₁ i t₂ > 0 ⇒ t₁t₂>0 i t₁+t₂>0 m < 2 z tego wychodzi No to mam już warunki mówiące, że funkcja ze zmienną t będzie miała dwa pierwiastki dodatnie, ale nie udowadnia mi to, że jeden z tych czterech pierwiastków funkcji ze zmienną x nie będzie równy drugiemu.

Jerzy: Nie ma takiej obawy, bo t₁ ≠ t₂

misio: No faktycznie, dzięki Jeszcze 3) x²−2m|x|+3m−2 = 0

	x2+3m−2
|x|=
	2m

x²−2m+3m−1=0 lub x²+2mx+3m−1=0 Δ=0 dla obu tych równań, wtedy każde z nich będzie miało jedno rozwiązanie. Co daje dwa rozwiązania do wyjściowego równania. Wychodzi że dla obu m wynosi

	3−√5
m1=
	2

	3+√5
m1=
	2

To są rozwiązania. Czy jeszcze trzeba uwzględnić, że rozwiązania są różne? W takim razie, wzór na x_o

2m		−2m
	≠
2		2

m≠0 Dobrze myślę?

Jerzy: Nie tak. x² = |x|² , czyli podstawiasz: |x| = t i t > 0

Jerzy: t² − 2mt + 3m − 2 = 0 musi mieć jedno dodatnie rozwiązanie

misio: Aaa dobra. Czyli

	1		7
m = −		lub m =
	2		2