Jak to zadanie zrobić wzorem herona? jacus: Punkt D leży na boku AB trójkąta ABC oraz |AC|=16, |AD|=6, |CD|=14 i |BC|=|BD|. Oblicz obwód trójkąta ABC. Jak to zadanie zrobić wzorem herona? (da się)

	16+6+x+x
p=		=11+x
	2

P=√(11+x)(11−16)(11−(6+x))(11−x) Nie ma chyba sensu dalej tego liczyć. Mógłby ktoś podpowiedzieć? Inne sposoby rozwiązania znam, chodzi mi tutaj o herona konkretnie.

fil: a co ci da ten heron tutaj?

jacus: No właśnie nie wiem, dlatego chciałbym się dowiedzieć. Wiem, że na 100% da się go tu zastosować i rozwiązać to zadanie w 3 minuty.

fil: Z innego sposobu da sie w 2 min

jacus: Wiem o tym. Znalazłem komentarz jak wykorzystać wzór herona: Masz 3 boki trójkąta ADC, więc możesz obliczyć jego pole P=24√3. Podstawiasz do wzoru 1/2 * a * h, gdzie a=6 (podstawa trójkąta). Wychodzi Ci wysokość i ta wysokość jest jednocześnie wysokością trójkąta ABC. Rysujesz sobie wysokość padającą na podstawę AB z punktu C i oznaczasz ten punkt np literą E. z pitagorasa liczysz odcinek AE i on wychodzi 8, zatem długość DB to x−2. No i pitagoras x² = h² + (x−2)² i masz x ładnie. Skąd niby wiadomo, że te dwa trójkąty mają tą samą wysokość?

fil:

jacus: Przecież ja obliczyłem wysokość tego trójkąta po prawo który ma boki 14, 16, 6, tak? Więc ta zaznaczona wysokość to nie jest jego, a całego trójkąta ABC.

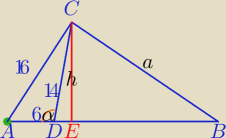
Mila: |DB|=a 1) P_ΔADC=24√3

	1
24√3=		*6*h⇔
	2

h=8√3 2) W ΔAEC: 16²=|AE|²+(8√3)² 256−192=|AE|² |AE|=8 |DE|=8−6=2 3) W ΔCEB: a²=h²+|EB|² a²=(8√3)²+(a−2)² a²=192+a²−4a+4 196=4a a=49 ============== II sposób− W ADC z tw. cosinusów 16²=6²+14²−2*6*14*cosα

	1
cosα=−
	7

W ΔCDB z tw. cosinusów: |CB|²=|CD|²+DB|²−2*|CD|*|BD|*cos(180−α)⇔

	1
a2=142+a2−2*14*a*
	7

196=4a a=49 obw_ΔABC=... ====