dowód algebraiczny salamandra: Wykaż, że dla dowolnych dodatnich liczb rzeczywistych x i y, takich, że x²+y²=2, prawdziwa jest nierówność x+y≤2 y²=2−x² y=√2−x² x+√2−x²≤2 / ² x²+2−x²≤4 2≤4 czy taki dowód też wszedłby w gre?

ICSP: (a+b)² ≠ a² + b² Proszę poprawić.

ICSP: a i dlaczego ruszasz obie strony tezy? Znów ten sam błąd

salamandra: Zrobiłem to inaczej, poprawnie, ale zastanawiałem się czy jakoś podstawiając y za x można to zrobić, co do błędu...kardynalny, zapomnijmy o tym

jc:

	(x+y)2+(x−y)2]		(x+y)2
Jeśli x+y > 2, to x2+y2 =		≥		> 4/2=2.
	2		2

ICSP: można to zrobić ale takie rozwiązanie nie będzie poprawne logicznie. x + √2 − x² ≤ 2 x² + 2x√2−x² + 2− x² ≤ 4 x√2−x² ≤ 1 x²(2−x²) ≤ 1 −x⁴ + 2x² − 1 ≤ 0 (x²−1)² ≥ 0

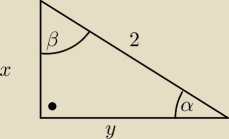
Maciess: Bez straty ogolnosci mozemy zalozyc, ze x,y sa bokami pewnego trojkąta prostokątnego. Wtedy mamy x=2sinα y=2sinB α+β=90^o

	α−β		α−β		90o
x+y=2(sinα+sinβ)=4(sin45o*cos(		)=2√2*cos(		)≤2√2*cos(		)=2
	2		2		2

Korzystasz z tego, że |α−β|≤90^o a cosinus jest parzysty

salamandra: ICSP dlaczego nie będzie poprawne logicznie?

Maciess: Nie zauważyłem ze w temacie jest dopisek dowód algebraiczny. Za swój bardzo przepraszam.

ICSP: Ponieważ przekształcasz tezę