Podaj zbiór wartości funkcji f(x) o określonej dziedzinie.
POMOCY: f(x) = log
2 x −> do każdego punktu wzór.
a) D
f = (0,1)
b) D
f = (2,
∞)
Jak to rozwiązać?
Podpunkt c ma takie dane:
I to potrafię rozwiązać.
Podstawiam do wzoru i wychodzi mi Y<−1,3>
A tutaj nie mam pojęcia jak.
Pomoże ktoś?
1 cze 00:36
Maciess: Co mozesz powiedziec o monotoniczności funkcji f?
1 cze 00:43
POMOCY: W którym podpunkcie? Jeśli chodzi o c no to rosnąca
1 cze 00:47
ICSP: f(x) = log2 (x) jest rosnąca w całej dziedzinie.
Interesuje Ciebie zachowanie tej funkcji w okolicy punktu 0 (prawa stron)
oraz co się z nią dzieje gdy x → ∞
Najlepiej jest narysować wykres.
1 cze 00:52
POMOCY: Nadal nie rozumiem. Podstawiam pod wzór dane z c i d i działa. W b podstawiając 2 też działa,
podstawijąc
∞ domyślam się że to będzie
∞. A w podpunkcie a nie mam pojęcia co wyjdzie z:
f(0) = log
2 0 =

1 cze 00:55
ICSP: ∞ to nie liczba nie możesz jej podstawić

log
2 0 nie jest określony (dziedzina logarytmu to x > 0)
Poniżej dołączam wykres.
1 cze 00:57
ICSP:
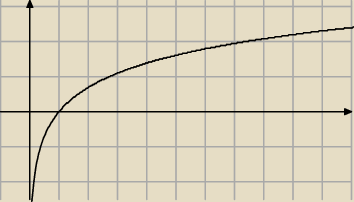
1 cze 00:57
ICSP: a) Df = (0,1)
Jakie wartości przyjmuje ta funkcja na przedziale (0;1) ?
1 cze 00:58
POMOCY: (−∞, 0)
1 cze 01:00
ICSP: dobrze.
Analogicznie robisz b)
Tylko musisz sprawdzić jaką wartość przyjmuje twoja funkcja dla x = 2
Mój rysunek jest tylko poglądowy i nie oddaje rzeczywistych wartości funkcji.
Jednak wiernie oddaje jej zachowanie.
1 cze 01:02
POMOCY: No ale jak ja mam to zrobić korzystając ze wzoru podanego w zadaniu? Pani przykładowy punkt
wykonała w taki sposób że podstawiła dwie wartości pod ten wzór i wyliczyła. Ale skoro nie
moge podstawić pod x ∞ oraz 0 to jak to zrobić?
1 cze 01:04
POMOCY: dla x = 2 wychodzi mi 1 bo log2 2 = 1 bo 21 to 2
1 cze 01:04
ICSP:
limx → 0+ f(x) = ?
limx → ∞ f(x) = ?
LUB
odczytujesz to wszystko z narysowanego wykresu.
1 cze 01:05

 log2 0 nie jest określony (dziedzina logarytmu to x > 0)
Poniżej dołączam wykres.
log2 0 nie jest określony (dziedzina logarytmu to x > 0)
Poniżej dołączam wykres.
