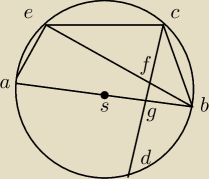
dowód geo marysia: Na okręgu o środku S wybrano punkty A ,B,C ,D ,E w ten sposób, że odcinek AB jest średnicą okręgu oraz |∡BCD | = |∡BEC | Wykaż, że proste AB i CD są prostopadłe AEB=90 stopni GFB=2α CFB=2α 4α=180 stopni 2α=90 stopni FGB=90 stopni cnd Dobrze to zrobiłam? Nie wiem czy tak zależność miedzy kątem środkowym i wpisanym tak działa, ale nie miałam innego pomysłu.

Qulka: coś z kosmosu ... kąt środkowy to taki który ma wierzchołek w środku okręgu czyli w S

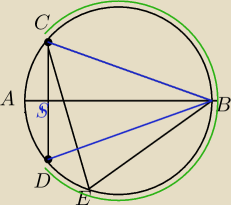
a7: łukDB=ŁukCB czyli |BD|=|CB| (gdyż kąty BCD oraz BEC są równe) więc także |AD|=|AC|, AB jest jedną z przekątnych deltoidu ADBC CD jest więc drugą przekątna tego deltoidu), nie wiem dokładnie jak należy zakońćzyć ten dowód, ale chodzi o równość odcinków BC i BD wynikającą z równości łuków mniiejszych BC i BD. AB jest średnicą, więć trójkąt DCB jestrównoramienny, a BS jest jego wyskością. c.n.w. coś w ten deseń

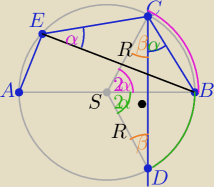
Eta: |∡BSC|=2*|∡BCE|= 2α i |∡DSB|=2*|∡BCD|=2α ΔDSC równoramienny to SB⊥CD więc AD ⊥CD c.n.w.

Eta: SB jest dwusieczną w trójkącie równoramiennym więc zawiera się w wysokości