Trójkąt Layla: Jak zrobić to zadanie? Wyznacz zbiór wszystkich punktów P należących do wnętrza trójkąta ABC, dla których P(△APC) = P(△BCP).

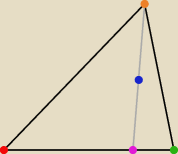
tuńczyk: Z góry przepraszam za brak podpisów na rysunku. Albo mój telefon nie jest w stanie ich dodać albo po prostu ja tego nie ogarniam. punkt A punkt B punkt C punkt D punkt P Punkt D − dowolny punkt na odcinku AB Oznaczam AD=y, DB=x 1) P△ADC=^y_xP△BDC //△ o wspólnej wysokości z C, ale różnych podstawach 2) Analogicznie P△ADP=^y_xP△BDP 3) Zatem P△APC= ^y_x(P△BDC−P△BDP)= ^y_xP△BPC Więc aby P△APC= P△BPC x=y Zatem jest to zbiór wszystkich punktów leżących na środkowej CM₃ i tylko tych punktów

Layla: Okej, dziękuje Jutro spróbuję to zrozumieć bo dziś to już nie jestem w stanie.