nierówności Mela: dana jest nierówność |x−1| + |x+2| <m wyznacz te wartości parametru m dla których ta nierówność nie ma rozwiązań

Izzy: Ludziska prosze jakąś wskazówke chociaż.

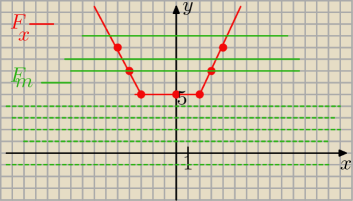
Eta: Najprościej poprzez narysowanie wykresów f(x) = |x+3|+ |x−2| −−−−−−−− czerwony f(x) = m −−−−−−− zielony wykres zielony nie może mieć punktów wspólnych z wykresem czerwonym a to jest dla m<5 Odp: dla m<5 nierówność nie ma rozwiązań wykresy częsciowe dla f(x) miejscami zerowymi pod modułami są x = −3 i x= 2 rozpatrujemy lewa stronę nierówności dla 1) x <−3 ( mamy zmianę znaków przy opuszczaniu modułów zatem ; f(x) = −x −3 −x +2 = −2x −1 2) dla x€<−3, 2) f(x)= x+3 −x +2 = 5 3) dla x€<2,∞) f(x) = x+3 +x −2 = 2x +1