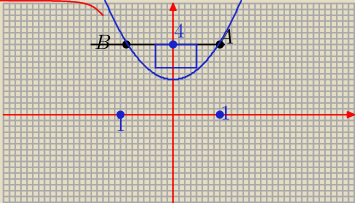
Rozważmy wszystkie prostokąty których dwa wierzchołki leżą na odcinku AB, Lewy18: Rozważmy wszystkie prostokąty których dwa wierzchołki leżą na odcinku AB,gdzie A=(−1,4) i B(4,1) a pozostałe dwa na paraboli o równaniu y=2x²+2.Wyznacz wymiary tego z prostokątów,który ma największe pole. Oblicz to pole. (Przepraszam za wysunek dopiero się uczę (ten prostokąt jest styczny to wykresu y=2x²+2 i do prostej y=4 Zadanie rozwiązałem ale zastanawiam się czemu krótszy bok prostokąta musi być w postaci −2x²+2 a nie 2x²−2 .Wtedy wiem że wyjdzie pole najmnijesze bo pochodna będzie skierowana ramionami w dół

fil: Krotszy bok masz: 4−2x²−2=−2x²−2

fil: +2 oczywiscie

ICSP: bo w przeciwnym wypadku nie będzie to prostokąt tylko trapez. P.S. Coś Ci te punkty się pomyliły.

Lewy18: fil a jakbym zapisał krótszy bok jako 2x²+2−4

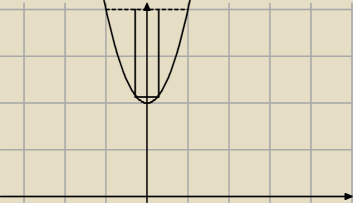
ICSP: "krótszy bok"

Lewy18: ICPS ,przyjacielu nie kwestionuje twoich zdolności artystycznych ,masz racje rzecz jasna chodzi mi tylko że uczono mnie że dł odcinka w geom.analitycznej wyznaczamy odejmujac obojetnie które wspolrzedne od ktorych np.PQ mozemy zapisac √(xp−xq) +(yp−yq) lub √(xq−xp) + (yq−yp) Pułapką w tym zadaniu jest że wtedy pochodna wychodzi wierzchołkiem do dołu i jej pole możemy wyliczyc najmniejsze a proszą nas o największe

fil: Pulapka jest uzycie tego wzoru w tym zadaniu

ICSP: Pokaz swoje długości boków Pokaż swoją pochodną.

Lewy18: dł bok=2x krótszy bok=2x²−2 Pochodna=12x²−4 ( o to mi chodzi wierzchołek jest na dole ramiona w górę pochodna pokazuje nam najmniejszą wartość) x=√3/3 i wychodzi to samo tylko pole jest wtedy najmniejsze i tu jest ten "myk"

ICSP: "krószy bok źle". Dla |x| < 1 dostajesz długości ujemne. "Krótsz bok": 4 − (2x² + 2) = 2 − 2x²

Lewy18: macie rację dopiero teraz to widze dziękuje ICPS i fil

salamandra: Na pewno dobre współrzędne punktów w ogóle podałeś?

Lewy18: B(1,4) pomyłka