Cosinus kąta między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego Maciek: Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego sześciokątnego, jeśli wiadomo że krawędź boczna jest trzy razy dłuższa od krawędzi podstawy.

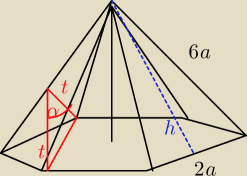
salamandra: h²+a²=36a² h=a√35

	2a*a√35
Pściany bocznej=		=a2√35
	2

Pole ściany na drugi sposób, gdzie t jest wysokością trójkąta, a 6a podstawą:

	6a*t
a2√35=
	2

a²√35=3a*t

	a√35
t=
	3

Z twierdzenia cosinusów w czerwonym trójkącie, który zawiera dwie wysokości trójkąta równobocznego w podstawie oraz ramiona długości "t"

	2a√3
2*		=2a√3
	2

	35		35		35a2
12a2=		a2+		a2−2*		*cosα
	9		9		9

	70		70
12a2=		a2−		a2*cosα
	9		9

38		9
	a2*		=cosα
9		−70a2

	19
cosα=−
	35