geomatria fil: Wyznacz równanie okregu wpisanego w deltoid, którego boki sa zawarte w prostych o równaniach x + 3 = 0, y + 2 = 0, x + 2y = 3 i y + 2x = 2.

lol: Proponuje ukladami rownan znalezc najpierw punkty przeciecia prostych. Nastepnie pole równolegloboku. A stad juz latwo promien.

lol: Poczatek bedzie taki:

⎧	x+3=0
⎩	y+2=0	Stad (−3,−2) itd. Narysuj sobie zeby to zobaczyc. Masz dwie proste prostopadle

do siebie.

fil: Juz dawno to zrobilem, jednak doszedlem do wniosku ze w tym zadaniu wyznaczenie wspolrzednych punktow deltoidu bedzie bezuzytezcne

fil: W sumie mozna wyznaczyc prosta, na ktorej bedzie lezec srodek tego okregu

lol:

	1
Z kolejnych wyjdzie Ci (2,−2) oraz (−3,3) oraz (1/3, 1		)
	3

lol: fakt mozna inaczej

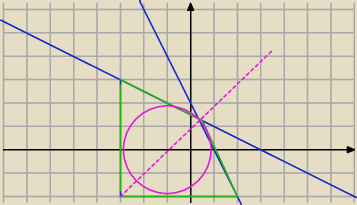
Qulka: za mała precyzja programu

Qulka: z odległości punktu od prostej

Qulka: a=(1−3√5)/(3+√5)