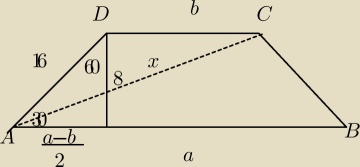
planimetria salamandra: W dany trapez można wpisać okrąg i jednocześnie można na tym trapezie opisać okrąg. Wysokość tego trapezu jest równa 8, a jego kąt ostry ma miarę 30 stopni. Oblicz długość promienia okregu opisanego na tym trapezie.

a−b
	=8√3
2

a−b=16√3 a=16√3+b Z warunku wpisywalności okregu w czworokąt: 16√3+2b=32 32−16√3=2b b=16−8√3 a=16√3+16−8√3=16+8√3 z tw. cosinusów w ΔADC x²=256+256−256√3+192−32(16−8√3)*cos150

	√3
x2=704−256√3−(512−256√3)*(−		)
	2

x²=704−256√3+256√3−384 x=8√5

x
	=2R
sin150

R=8√5 jest ok?

ICSP: a + b = 32

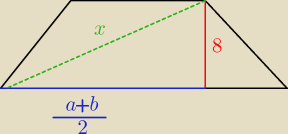
a + b
	= 16
2

h = 8 x = √ 16² + 8² = 8√2² + 1 = 8√5 Trochę szybciej obliczone. No i bez wykorzystywania twierdzenia cosinusów.

salamandra: właśnie na początku miałem taki zamysł, nie wiem czemu w tę stronę nie poszedłem, dzięki w każdym razie