Planimetria
dexter:
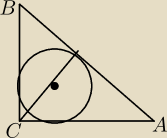
Dany jest trójkąt prostokątny ABC , w którym BC = 30 , AC = 40 i AB = 50 . Okrąg wpisany w
trójkąt ABC jest styczny do boku AB w punkcie M . Oblicz długość odcinka CM
Mogę to zadanie zrobić twierdzeniem Stewarta? Gdy robię go tym twierdzeniem wynik wychodzi inny
29 maj 16:18
a7:
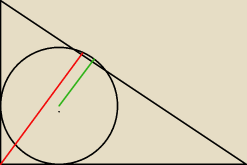
na Twoim rysunku wygląda jakby czewiana CM pokrywała się z odcinkiem od środka okręgu do AB,
tak nie jest, więc chyba tj. moim bardzo skromnym zdaniem (gdyż nie znałam wcześniej tego tw.)
twierdzeniem Stewarta w prosty sposób tego nie załatwisz
29 maj 16:38
a7: źle przeczytałam treść zadania,
29 maj 16:41
a7:
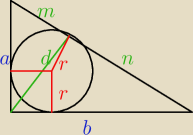
r=10
m=30−10=20 n=40−10=30
z tw. Stewarta
a
2*n+b
2*m=c(d
2+m*n)
900*30+1600*20=50(d
2+600)
d
2=580
d=2
√145

29 maj 16:48
a7: jaki powinien być wynik?
29 maj 16:49
a7: II sposób
cosCBA=3/5
r=10 m=20 a=30
z tw. cosinusów
d2=a2+m2−2amcosCBA
d2=580
d=...
zgodziło się
29 maj 16:53
Eta:
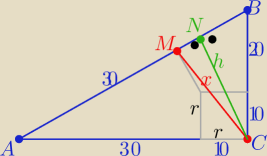
2r=30+40−50 ⇒ r=10
P(ABC)= 600 i P(ABC)= 25*h ⇒
h=24
w ΔCBN : |NB|=
√302−242 ⇒ |NB|=18
to |MN|=20−18=2
i z tw. Pitagorasa w ΔMNC
x=
√242+22=
√580
x= 2
√145
=========
29 maj 16:56
Eta:
Najprostszy jest
II sposób podany przez
a7 
29 maj 17:02
a7: wow chyba moje pierwsze jabłuszko

, a ja myślałam, że ewentualnie będzie cóś na
temat kiepskawych rysunków....
29 maj 17:06
Eta:
Aż taka "groźna" jestem ?

Mój sposób dla SP ( bez Stewarta i trygonometrii i tylko Pitagoras

29 maj 17:34
dexter: Czemu m=20, a n=30? Ja wzialem, że m=30 n=20, w jaki sposob okreslic ktore to m, a ktore to n?
29 maj 18:19
a7:
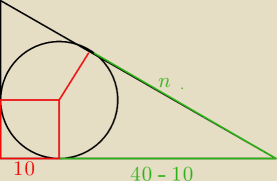
29 maj 18:23
a7: oznaczasz jak chcesz tylko potem trzeba prawidłowo podstawić do wzoru
29 maj 18:23
dexter: Faktycznie, źle podstawiłem... dzięki

29 maj 18:26
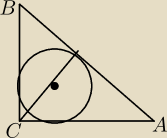 Dany jest trójkąt prostokątny ABC , w którym BC = 30 , AC = 40 i AB = 50 . Okrąg wpisany w
trójkąt ABC jest styczny do boku AB w punkcie M . Oblicz długość odcinka CM
Mogę to zadanie zrobić twierdzeniem Stewarta? Gdy robię go tym twierdzeniem wynik wychodzi inny
Dany jest trójkąt prostokątny ABC , w którym BC = 30 , AC = 40 i AB = 50 . Okrąg wpisany w
trójkąt ABC jest styczny do boku AB w punkcie M . Oblicz długość odcinka CM
Mogę to zadanie zrobić twierdzeniem Stewarta? Gdy robię go tym twierdzeniem wynik wychodzi inny
 na Twoim rysunku wygląda jakby czewiana CM pokrywała się z odcinkiem od środka okręgu do AB,
tak nie jest, więc chyba tj. moim bardzo skromnym zdaniem (gdyż nie znałam wcześniej tego tw.)
twierdzeniem Stewarta w prosty sposób tego nie załatwisz
na Twoim rysunku wygląda jakby czewiana CM pokrywała się z odcinkiem od środka okręgu do AB,
tak nie jest, więc chyba tj. moim bardzo skromnym zdaniem (gdyż nie znałam wcześniej tego tw.)
twierdzeniem Stewarta w prosty sposób tego nie załatwisz
 r=10
m=30−10=20 n=40−10=30
z tw. Stewarta
a2*n+b2*m=c(d2+m*n)
900*30+1600*20=50(d2+600)
d2=580
d=2√145
r=10
m=30−10=20 n=40−10=30
z tw. Stewarta
a2*n+b2*m=c(d2+m*n)
900*30+1600*20=50(d2+600)
d2=580
d=2√145

 2r=30+40−50 ⇒ r=10
P(ABC)= 600 i P(ABC)= 25*h ⇒ h=24
w ΔCBN : |NB|= √302−242 ⇒ |NB|=18
to |MN|=20−18=2
i z tw. Pitagorasa w ΔMNC
x=√242+22=√580
x= 2√145
=========
2r=30+40−50 ⇒ r=10
P(ABC)= 600 i P(ABC)= 25*h ⇒ h=24
w ΔCBN : |NB|= √302−242 ⇒ |NB|=18
to |MN|=20−18=2
i z tw. Pitagorasa w ΔMNC
x=√242+22=√580
x= 2√145
=========

 , a ja myślałam, że ewentualnie będzie cóś na
temat kiepskawych rysunków....
, a ja myślałam, że ewentualnie będzie cóś na
temat kiepskawych rysunków....
 Mój sposób dla SP ( bez Stewarta i trygonometrii i tylko Pitagoras
Mój sposób dla SP ( bez Stewarta i trygonometrii i tylko Pitagoras 

