))) Kostewycz Marta: Napisz wzory prostych symetrycznych do danej prostej a: względem osi x (prostą m) oraz względem osi y (prostą k), gdy prosta a ma wzór: 1)a: y = −2x + 4 2)a: y = x − 5

wredulus_pospolitus: funkcja symetryczna względem osi OX powstaje poprzez wstawienie (−x) w miejsce każdego 'x' więc y = −2*(−x) + 4 czyli y = 2x + 4 funkcja symetryczna względem osi OY powstaje poprzez wstawienie − przed cały wzór funkcji więc y = − (−2x + 4) czyli y = 2x − 4

Kostewycz Marta: a drugie?

wredulus_pospolitus: drugi przykład zrób ANALOGICZNIE ... przeczytaj ze zrozumieniem co napisałem i zrób DOKŁADNIE to samo co zrobiłem

Jerzy: Bleee,chyba pomyliłeś osie

Kostewycz Marta: Jerzy, pomóż mi, proszę CI bardzo

Jerzy: Jest tak,jak napisał Bleee,tylko odwrotnie.Tam gdzie napiał OX powinno być OY i odwrotnie.

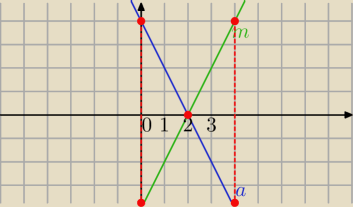
Mila: 1)a: y = −2x + 4 symetria względem OX m: y=−(−2x+4)⇔y=2x−4

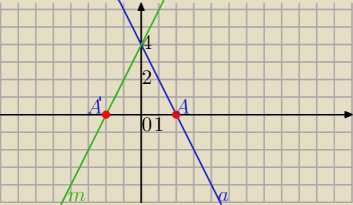
Mila: 1)a: y = −2x + 4 symetria względem OY m: y=−2*(−x) +4 ⇔ y=2x+4

Mila: 2) a: y = x − 5 symetria względem OX m: y=−(x−5)⇔ y=−x+5 symetria względem OY n: y= −x−5