w Trójkącie ABC punkt D należy do boku AC i |AD| : |DC| = 1:3, na boku BC dany j geometria: w Trójkącie ABC punkt D należy do boku AC i |AD| : |DC| = 1:3, na boku BC dany jest punkt E taki,że |CE| : |EB| = 4:1. Punkt F jest punktem przecięcia odcinków BD i AE. Oblicz pole trójkąta ABC wiedząc, ze pole trójkąta ACF jest równe 2.

Eta: P(ABC)=34

geometria: jest szansa na wytłumaczenie?

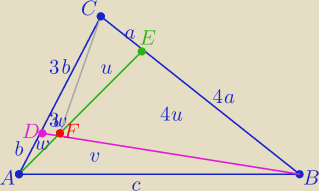
Eta: 4w=2 ⇒ w=1/2 w ΔACE i ABE : 4(4w+u)= v+4u ⇒ v=16w w ΔABD i BCD : 3(w+v)=5u+3w ⇒ 3v=5u ⇒ 5u=48w P(ABC)= 4w+v+5u = 68w = 34