Planimetria
Jabłecznik:
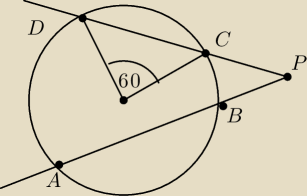
Treść: Oblicz długość odcinka |PC| jeżeli wiadomo, że |AB|=2|CD| oraz |BP|+2=|CP| oraz promień
okręgu wynosi 10.
Dobrze rozwiązałem?
Twierdzenie o siecznych: |CD|*|CP|=|AB|*|BP|
|CD|*|CP|=|AB|*(|CP|−2)
...
Czy |CP|=40?
28 maj 11:21
a7:
|CP|*|CD|=|AB|*|BP|
|CP|*|CD|=2*|CD|*(|CP|−2)
|CP|=2(|CP|−2)
|CP|=2|CP|−4
|CP|=4
tylko nie rozumiem po co informacja o promieniu okręgu, nie wiem czy czegoś nie przeoczyłam?
28 maj 11:33
ICSP: Proszę zapoznać się z prawidłową wersją twierdzenia o siecznych.
28 maj 11:40
janek191:
I CD I = r = 10
I AB I = 2*10 = 20
I CP I = x
I BP I = x − 2
więc
x*( 10 + x) = (x −2)*( 20 + x − 2)
x2 + 10 x = (x −2)*(x + 18)
x2 + 10 x = x2 +16 x −36
− 6 x = − 36
x = 6
=====
I CP I = 6
28 maj 11:42
a7:
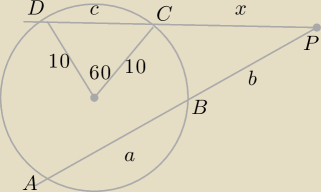
jasne już mam
|PA|*|BP|=|PD|*|PC|
(|PC|−2+2|CD|)*(|PC|−2)=((|PC|+|CD|)(|PC|)
CD=c=10
(x−2+2*10)(x−2)=(x+10)x
(x+18)(x−2)=x
2+10x
x
2−2x+18x−36=x
2+10x
6x=36
x=6
===
28 maj 11:57
 Treść: Oblicz długość odcinka |PC| jeżeli wiadomo, że |AB|=2|CD| oraz |BP|+2=|CP| oraz promień
okręgu wynosi 10.
Dobrze rozwiązałem?
Twierdzenie o siecznych: |CD|*|CP|=|AB|*|BP|
|CD|*|CP|=|AB|*(|CP|−2)
...
Czy |CP|=40?
Treść: Oblicz długość odcinka |PC| jeżeli wiadomo, że |AB|=2|CD| oraz |BP|+2=|CP| oraz promień
okręgu wynosi 10.
Dobrze rozwiązałem?
Twierdzenie o siecznych: |CD|*|CP|=|AB|*|BP|
|CD|*|CP|=|AB|*(|CP|−2)
...
Czy |CP|=40?
 jasne już mam
|PA|*|BP|=|PD|*|PC|
(|PC|−2+2|CD|)*(|PC|−2)=((|PC|+|CD|)(|PC|)
CD=c=10
(x−2+2*10)(x−2)=(x+10)x
(x+18)(x−2)=x2+10x
x2−2x+18x−36=x2+10x
6x=36
x=6
===
jasne już mam
|PA|*|BP|=|PD|*|PC|
(|PC|−2+2|CD|)*(|PC|−2)=((|PC|+|CD|)(|PC|)
CD=c=10
(x−2+2*10)(x−2)=(x+10)x
(x+18)(x−2)=x2+10x
x2−2x+18x−36=x2+10x
6x=36
x=6
===