 czy tam ma być przecinek? (bc=2,
as=20)
Wysokość jest prostopadła do |BC| czyli z pitagorasa:
H2+102=(2√194)2
H=26
Teraz chciałem policzyć wysokość podstawy czyli ΔABC:
h2+102=262
h=24
czy tam ma być przecinek? (bc=2,
as=20)
Wysokość jest prostopadła do |BC| czyli z pitagorasa:
H2+102=(2√194)2
H=26
Teraz chciałem policzyć wysokość podstawy czyli ΔABC:
h2+102=262
h=24
| 1 | ||
Pp= | *20*24=240 | |
| 2 |
| 1 | ||
V= | *240*26=2059,2 | |
| 3 |
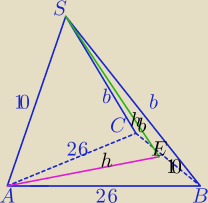 W treści nie masz informacji z której możesz od razu ustalić, gdzie leży spodek wysokości
ostrołupa.
Ostrosłup jest "przechylony" w stronę lewą, Krawędź AS jest najkrótsza.
1) Musimy sprawdzić, czy jedna z krawędzi nie jest prostopadła do płaszczyzny .
2) jeśli nie jest, to będziemy myśleć dalej.
Prostopadła może być tylko AS
|AS|=10, |BC|=20
b=2√194
3) h=24
ΔACS≡ΔABS
262+102≠(2√194)2⇒trójkąty nie są prostokątne
4) ΔAES:
hb2=(2√194)2−102=4*194−100=676
hb=26
hb2=676 i |AS|2+h2=102+242=676⇔
AS⊥AE
H=10− wysokość ostrosłupa
dalej licz sam
W treści nie masz informacji z której możesz od razu ustalić, gdzie leży spodek wysokości
ostrołupa.
Ostrosłup jest "przechylony" w stronę lewą, Krawędź AS jest najkrótsza.
1) Musimy sprawdzić, czy jedna z krawędzi nie jest prostopadła do płaszczyzny .
2) jeśli nie jest, to będziemy myśleć dalej.
Prostopadła może być tylko AS
|AS|=10, |BC|=20
b=2√194
3) h=24
ΔACS≡ΔABS
262+102≠(2√194)2⇒trójkąty nie są prostokątne
4) ΔAES:
hb2=(2√194)2−102=4*194−100=676
hb=26
hb2=676 i |AS|2+h2=102+242=676⇔
AS⊥AE
H=10− wysokość ostrosłupa
dalej licz sam